Вариант 2 Контрольная работа 4 ГДЗ Самостоятельные и контрольные работы Босова 8 класс (Информатика)
ВАРИАНТ 2 Для издания 2025 года: 1. У исполнителя Вычислитель две команды, которым присвоены номера: 1. умножь на 5 2. вычти 5 Первая из них увеличивает число в 5 раз, вторая уменьшает его на 5.



Ниже вариант решения задания из учебника Босова, Босова, Бондарева 8 класс, Просвещение:
ВАРИАНТ 2
Для издания 2025 года:
1. У исполнителя Вычислитель две команды, которым присвоены номера:
1. умножь на 5
2. вычти 5
Первая из них увеличивает число в 5 раз, вторая уменьшает его на 5. Составьте алгоритм получения из числа 4 числа 25, содержащий не более пяти команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.
1 – умножь на 5
2 – вычти 5
Данное задание удобно решать с «с заду на перед», от 25 к 4 или построить дерево решения.
4 – 20 – 15 – 10 – 5 – 25
Ответ: 12221
Для издания 2018 года:
1. У исполнителя Вычислитель две команды, которым присвоены номера: 1 — умножь на 5; 2 — вычти 5.
Первая из них увеличивает число в 5 раз, вторая уменьшает его на 5. Составьте алгоритм получения из числа 4 числа 80, содержащий не более пяти команд. В ответе запишите только номера команд. Если таких алгоритмов более одного, то запишите любой из них.
1 – умножь на 5
2 – вычти 5
Данное задание удобно решать с «с заду на перед», от 80 к 4.
Если построить дерево, то видно, что за 5 команд не получается получить из 4 число 80. Можно за 6 команд.
112222 (4 – 20 – 100 – 95 – 90 – 85 – 80)
Ответ: 112222
Для издания 2025 года:
2. Чертёжнику был дан для исполнения следующий алгоритм:
Команда 1
Повтори 5 раз
Сместиться на (-2, -1)
Сместиться на (12, 10)
Конец
Какой должна быть Команда 1, чтобы Чертёжник вернулся в исходную точку, из которой он начал движение?
Для возврата в исходную точку общее смещение и по Х, и по У должно равняться 0.
Смещение по Х:
а + 5*(-2 + 12) = а – 10 + 60 = 0; а = -50
Смещение по У:
с + 5*(-1 + 10) = с – 5 + 50 = 0; с = -45
Ответ: сместиться на (-50, -45)
Для издания 2018 года:
2. Чертёжнику был дан для исполнения следующий алгоритм:
Команда 1
Повтори 5 раз
Сместиться на (-2, -1)
Сместиться на (2, 1)
Конец
Какой должна быть Команда 1, чтобы Чертёжник вернулся в исходную точку, из которой он начал движение?
Для возврата в исходную точку общее смещение и по Х, и по У должно равняться 0.
Смещение по Х:
а + 5*(-2 + 2) = а – 10 + 10 = 0; а = 0
Смещение по У:
с + 5*(-1 + 1) = с – 5 + 5 = 0; с = 0
Ответ: сместиться на (0, 0)
Для издания 2025 года:
3. Определите значение переменной а после исполнения следующего алгоритма.
а := 3
b := 50
а := b / 5 * а
b := 9 + а * b L...і.
Порядок действий соответствует правилам арифметики.
a: = 3
b: = 50
a: = b:5*a (50/5*3 = 30)
b: = 9 + a*b (9 + 30*50 =1509)
Ответ: 30
Для издания 2018 года:
3. Автомат получает на вход пятизначное десятичное число. По полученному числу строится новое десятичное число по следующему правилу.
1) Вычисляются два числа — сумма первой, третьей и пятой цифр и сумма второй и четвёртой цифр заданного числа.
2) Полученные два числа записываются друг за другом в порядке неубывания (без разделителей).
Пример: исходное число: 14351. Поразрядные суммы: 5, 9.
Результат: 95.
Определите, сколько из приведённых ниже чисел может получиться в результате работы автомата.
30 1528 116 1519 2019 1920 1915 316 2815
Для издания 2025 года:
4. Автомат получает на вход пятизначное десятичное число. По полученному числу строится новое десятичное число по следующему правилу:
1) вычисляются два числа — сумма первой, третьей и пятой цифр и сумма второй и четвёртой цифр заданного числа;
2) полученные два числа записываются друг за другом в порядке неубывания (без разделителей).
Пример: исходное число: 14351. Поразрядные суммы: 5, 9.
Результат: 95.
Определите, сколько из приведённых ниже чисел может получиться в результате работы автомата.
30 1528 116 1519 2019 1920 1915 316 2815
Сумма трех цифр не может превышать 27 (9+9+9 = 27), а двух 18 (9+9 = 18)
30 (10101), 1528, 116 (13931), 1519, 2019, 1920, 1915 (97981), 316, 2815
Ответ: 3
Для издания 2018 года:
4. Определите значение переменной а после исполнения следующего алгоритма.
а:=3
b:=50
а:=Ь:5*а
b:=9+а*b
Порядок действий соответствует правилам арифметики.
a: = 3
b: = 50
a: = b:5*a (50/5*3 = 30)
b: = 9 + a*b (9 + 30*50 =1509)
Ответ: 30
5. Определите значение переменной d после исполнения следующего алгоритма, если переменным а, b, с были присвоены значения 100, 12 и 100 соответственно.
Ответ: 12
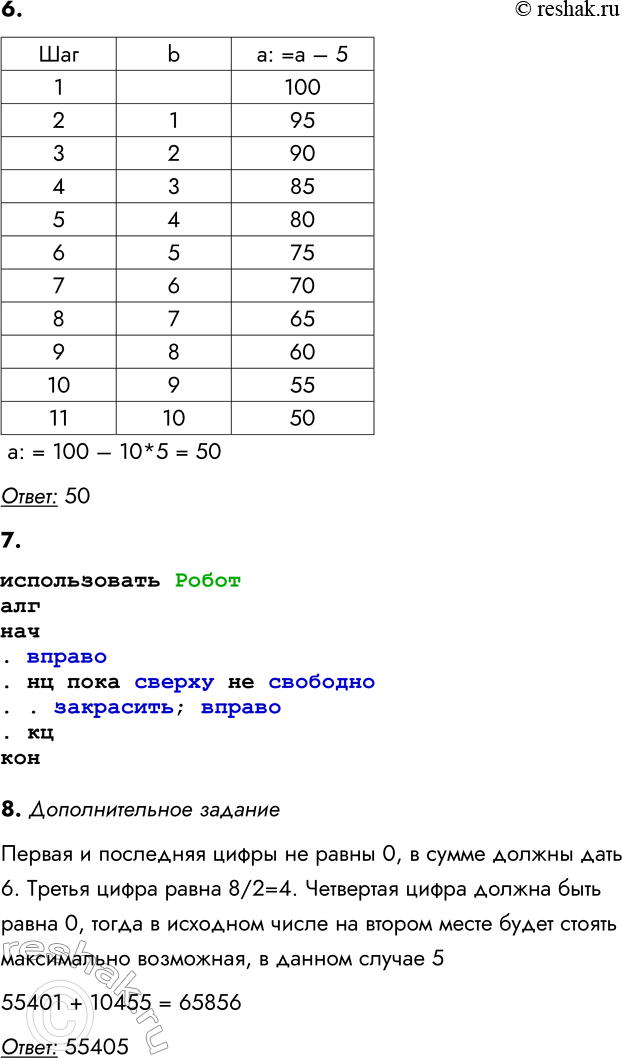
6. Запишите значение переменной а, полученное в результате выполнения следующего алгоритма.
а: = 100
нц для b от 1 до 10
а : = а - 5
кц
а: = 100 – 10*5 = 50
Ответ: 50
7. На бесконечном клетчатом поле находится длинная горизонтальная стена. Длина стены неизвестна. Робот (обозначен ромбом) находится в закрашенной клетке под стеной.
Робот должен закрасить все клетки, прилегающие к горизонтальной стене снизу (так, как это изображено на рисунке ниже). Конечное положение Робота значения не имеет.
Правильность алгоритма проверьте в среде КуМир.
использовать Робот
алг
нач
. вправо
. нц пока сверху не свободно
. . закрасить; вправо
. кц
кон
8. Дополнительное задание. К пятизначному нечётному натуральному числу применяется следующий алгоритм.
1) Записать цифры исходного числа в обратном порядке.
2) Сложить получившееся число с исходным числом.
Пример работы алгоритма для числа 22011:
22011 + 11022 = 33033.
Укажите наибольшее пятизначное нечётное число, в результате применения к которому данного алгоритма получится число 65856.
Первая и последняя цифры не равны 0, в сумме должны дать 6. Третья цифра равна 8/2=4. Четвертая цифра должна быть равна 0, тогда в исходном числе на втором месте будет стоять максимально возможная, в данном случае 5
55401 + 10455 = 65856
Ответ: 55405
