Дополнительное задание 2 Параграф 27 ГДЗ Семакин 8 класс (Информатика)
ЕК ЦОР: Часть2, глава 6, §39. ЦОР № 13, 14, 15 Практическое задание №23 Тема: Использование циклов в вычислительных алгоритмах 1 уровень сложности 1.
















Ниже вариант решения задания из учебника Семакин, Залогова 8 класс, Просвещение:
ЕК ЦОР: Часть2, глава 6, §39. ЦОР № 13, 14, 15
Практическое задание №23
Тема: Использование циклов в вычислительных алгоритмах
1 уровень сложности
1. Разработать схему алгоритма, который запрашивает N произвольных целых чисел и ищет их сумму. Число N вводится с клавиатуры. Разработать для созданного алгоритма не менее трёх тестов и проверить на них правильность работы алгоритма.
2. Разработать схему алгоритма для вычисления суммы ряда:
Число N вводится с клавиатуры.
Протестировать алгоритм для N=1, N=2, N=4, N=6. Правильность ответов проверить с помощью калькулятора.
3. Одноклеточная амёба каждые три часа делится на 2 клетки. Разработать схему алгоритма для определения, сколько амёб будет через 3, 6, 9, 12 и 24 часа.
4. Дано натуральное число N и действительное число x. Разработать схему алгоритма для вычисления суммы ряда:
sin x + sin 2x+sin 3x+…sin N*X
Протестировать алгоритм для x=1.5 и N=3. Проверить правильность ответа на калькуляторе.
5. Разработать схему алгоритма для вычисления N-ой степени числа a (aN). Протестировать алгоритм для а) a=3 и N=4, б) a=2 и N=5.
1.
алг
нач
. цел n,s,a
. ввод n
. s:=0
. нц n раз
. . ввод a
. . s:=s+a
. кц
. вывод s
кон
2.
алг
нач
. цел n,i
. вещ s
. ввод n
. s:=0; i:=0
. нц n раз
. . i:=i+1
. . s:=s+1/i
. кц
. вывод s
кон
3.
алг
нач
. цел t,n,i
. ввод t
. n:=1;i:=0
. нц пока i
. . n:=n*2
. . i:=i+3
. кц
. вывод n
кон
4.
алг
нач
. цел n,i
. вещ x,a,s
. ввод n
. ввод x
. s:=0; a:=x;i:=0;
. нц n раз
. . i:=i+1
. . x:=a*i
. . s:=s+sin(x)
. кц
. вывод s
кон
5.
алг
нач
. цел n,a,st,i
. ввод n,a
. i:=0;st:=1
. нц n раз
. . i:=i+1
. . st:=st*a
. кц
. вывод st
кон
2 уровень сложности
1. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10% нормы предыдущего дня. Какой суммарный путь пробежит спортсмен за N дней? Разработать схему алгоритма для решения этой задачи. Протестировать алгоритм для N=3 и N=7.
2. Ежемесячная стипендия студента составляет A рублей в месяц, а расходы на проживание превышают стипендию и составляют B рублей в месяц. Рост цен ежемесячно увеличивает расходы на 3%. Разработать схему алгоритма для расчёта необходимой суммы денег, которую надо единовременно попросить у родителей, чтобы можно было прожить учебный год (10 месяцев), используя только эти деньги и стипендию. Протестировать алгоритм для следующих исходных данных:
а) A=1000, B=1100
б) A=900, B=1000
в) A=600, B=1200
3. Разработать схему алгоритма для нахождения всех делителей натурального числа N. Протестировать алгоритм для N=10, N=75, N=99, N=13.
4. Разработать схему алгоритма для вычисления N! (факториал числа N). Факториал вычисляется по формуле:
N!=
Операцию вычисления факториала использовать нельзя!
Протестировать алгоритм для N=0, N=2 N=4.
1.
алг
нач
. цел n,i
. вещ s,a
. ввод n
. a:=10;s:=a
. нц n-1 раз
. . a:=a*1.1
. . s:=s+a
. кц
. вывод s
кон
2.
алг
нач
. цел n
. вещ s,b
. ввод n |стипендия
. ввод b |расход за первый месяц
. s:=b
. нц 9 раз
. . b:=b*1.03
. . s:=s+b
. кц
. вывод s-n*10|взнос родителей
кон
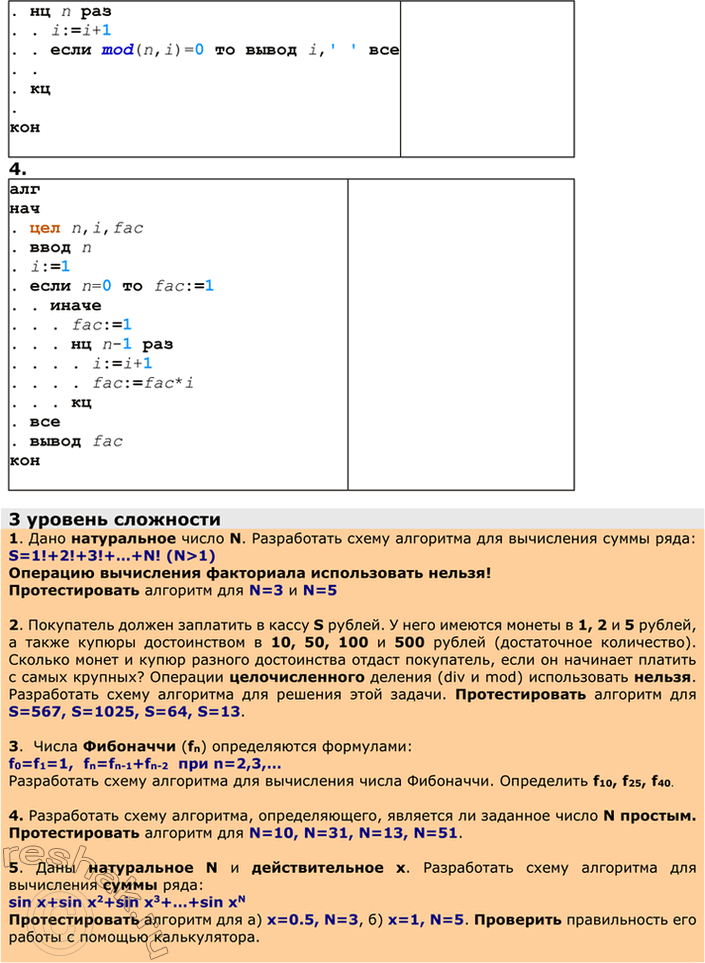
3.
алг
нач
. цел n,i
. ввод n
. i:=0
. нц n раз
. . i:=i+1
. . если mod(n,i)=0 то вывод i,task task все
. .
. кц
.
кон
4.
алг
нач
. цел n,i,fac
. ввод n
. i:=1
. если n=0 то fac:=1
. . иначе
. . . fac:=1
. . . нц n-1 раз
. . . . i:=i+1
. . . . fac:=fac*i
. . . кц
. все
. вывод fac
кон
3 уровень сложности
1. Дано натуральное число N. Разработать схему алгоритма для вычисления суммы ряда: S=1!+2!+3!+…+N! (N > 1)
Операцию вычисления факториала использовать нельзя!
Протестировать алгоритм для N=3 и N=5
2. Покупатель должен заплатить в кассу S рублей. У него имеются монеты в 1, 2 и 5 рублей, а также купюры достоинством в 10, 50, 100 и 500 рублей (достаточное количество). Сколько монет и купюр разного достоинства отдаст покупатель, если он начинает платить с самых крупных? Операции целочисленного деления (div и mod) использовать нельзя. Разработать схему алгоритма для решения этой задачи. Протестировать алгоритм для S=567, S=1025, S=64, S=13.
3. Числа Фибоначчи (fn) определяются формулами:
f0=f1=1, fn=fn-1+fn-2 при n=2,3,…
Разработать схему алгоритма для вычисления числа Фибоначчи. Определить f10, f25, f40.
4. Разработать схему алгоритма, определяющего, является ли заданное число N простым. Протестировать алгоритм для N=10, N=31, N=13, N=51.
5. Даны натуральное N и действительное x. Разработать схему алгоритма для вычисления суммы ряда:
sin x+sin x2+sin x3+…+sin xN
Протестировать алгоритм для а) x=0.5, N=3, б) x=1, N=5. Проверить правильность его работы с помощью калькулятора.
1.
алг
нач
. цел n,i,j,fac,s
. ввод n
. i:=0
. s:=0
. нц n раз
. . i:=i+1
. . fac:=1
. . j:=0
. . нц i раз
. . . j:=j+1
. . . fac:=fac*j
. . кц
. . s:=s+fac
. кц
. вывод s
кон
2.
алг
нач
. цел s,k500,k100,k50,k10,m5,m2,m1
. k500:=0; k100:=0;k50:=0;k10:=0
. m5:=0;m2:=0;m1:=0
. ввод s
. нц пока s-500 > =0
. . k500:=k500+1
. . s:=s-500
. кц
. нц пока s-100 > =0
. . k100:=k100+1
. . s:=s-100
. кц
. нц пока s-50 > =0
. . k50:=k50+1
. . s:=s-50
. кц
. нц пока s-10 > =0
. . k10:=k10+1
. . s:=s-10
. кц
. нц пока s-5 > =0
. . m5:=m5+1
. . s:=s-5
. кц
. нц пока s-2 > =0
. . m2:=m2+1
. . s:=s-2
. кц
. m1:=s
. вывод task500 > task,k500,task task
. вывод task100 > task,k100,task task
. вывод task50 > task,k50,task task
. вывод task10 > task,k10,task task
. вывод task5 > task,m5,task task
. вывод task2 > task,m2,task task
. вывод task1 > task,m1,task task
кон
3.
алг
нач
. цел n,f,f1,f2,i
. ввод n
. если n=0 или n=1 то f:=1
. . иначе
. . . f1:=1;f2:=1; i:=1
. . . нц n-1 раз
. . . . f:=f1+f2
. . . . f1:=f2;f2:=f
. . . кц
. все
. вывод f
кон
4.
алг
нач
. цел n,f,i
. ввод n
. i:=1;f:=1
. нц n-2 раз
. . i:=i+1
. . если mod(n,i)=0 то f:=0 все
. . вывод n,task task,i,task;task
. кц
. если f=1 то вывод taskпростоеtask
. . иначе вывод taskне простоеtask
. все
.
кон
5.
алг
нач
. цел n
. вещ x,s,a
. ввод n,x
. a:=x;s:=0
. нц n раз
. . s:=s+sin(x)
. . x:=x*a
. кц
. вывод s
.
кон
Практическое задание №24
Тема: Программирование циклов на Паскале
1 уровень сложности
1. Написать на Паскале программу, которая запрашивает с клавиатуры N произвольных целых чисел и ищет их сумму. Число N вводится с клавиатуры. Разработать для созданной программы не менее трёх тестов и проверить на них правильность работы алгоритма.
2. Составить на Паскале программу для вычисления суммы ряда:
Число N вводится с клавиатуры.
Протестировать программу для N=1, N=2, N=4, N=6. Правильность ответов проверить с помощью калькулятора.
3. Одноклеточная амёба каждые три часа делится на 2 клетки. Определить, сколько амёб будет через 3, 6, 9, 12 и 24 часа.
4. Дано натуральное число N и действительное число x. Вычислить сумму ряда:
sin x + sin 2x+sin 3x+…sin N*X
Протестировать программу для x=1.5 и N=3. Проверить правильность ответа на калькуляторе.
5. Написать программу для вычисления N-ой степени числа a (aN). Протестировать программу для а) a=3 и N=4, б) a=2 и N=5.
1.
program task_1;
var
i, n, s, a: integer;
begin
write(taskN > task);
readln(n);
s := 0;
for i := 1 to n do
begin
write("a > ");
readln(a);
s := s + a
end;
writeln(taskSUM=task, s)
end.
2.
program task_2;
var
i, n: integer;
s: real;
begin
write(taskN > task);
readln(n);
s := 1;
for i := 2 to n do
s := s + 1 / i;
writeln(taskSUM=task, s:5:2)
end.
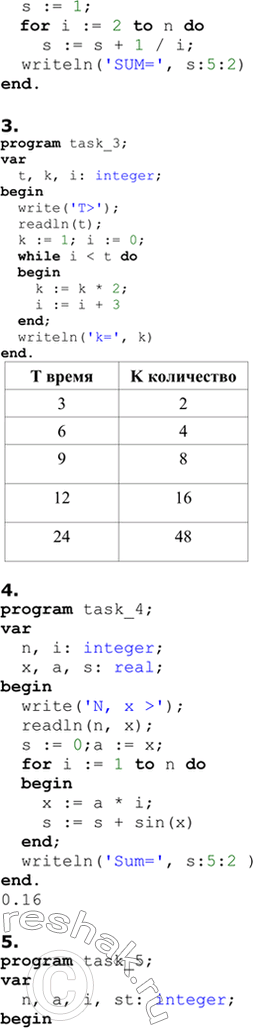
3.
program task_3;
var
t, k, i: integer;
begin
write(taskT > task);
readln(t);
k := 1; i := 0;
while i
begin
k := k * 2;
i := i + 3
end;
writeln(taskk=task, k)
end.
T время K количество
3 2
6 4
9 8
12 16
24 48
4.
program task_4;
var
n, i: integer;
x, a, s: real;
begin
write(taskN, x > task);
readln(n, x);
s := 0;a := x;
for i := 1 to n do
begin
x := a * i;
s := s + sin(x)
end;
writeln(taskSum=task, s:5:2 )
end.
0.16
5.
program task_5;
var
n, a, i, st: integer;
begin
write(taskВведи a и N через пробел > > task);
readln(a, n);
st := 1;
for i := 1 to n do
st := st * a;
writeln(a, task в степени task, n, task = task, st)
end.
2 уровень сложности
1. Начав тренировки, спортсмен в первый день пробежал 10 км. Каждый день он увеличивал дневную норму на 10% нормы предыдущего дня. Какой суммарный путь пробежит спортсмен за N дней? Протестировать программу для N=3 и N=7.
2. Составить программу, которая печатает таблицу умножения и таблицу сложения для числа N в десятичной системе счисления. Протестировать программу для чисел 6 и 9.
3. Составить программу, которая запрашивает пароль (четырёхзначное число) до тех пор, пока он не будет правильно введён. Протестировать программу.
4. Ежемесячная стипендия студента составляет A рублей в месяц, а расходы на проживание превышают стипендию и составляют B рублей в месяц. Рост цен ежемесячно увеличивает расходы на 3%. Составить программу расчёта необходимой суммы денег, которую надо единовременно попросить у родителей, чтобы можно было прожить учебный год (10 месяцев), используя только эти деньги и стипендию. Протестировать программу для следующих исходных данных:
а) A=1000, B=1100
б) A=900, B=1000
в) A=600, B=1200
5. Найти все делители натурального числа N. Протестировать программу для N=10, N=75, N=99, N=13.
6. Написать программу вычисления N! (факториал числа N). Факториал вычисляется по формуле:
N!=
Протестировать программу для N=0, N=2 N=4.
1.
program task_1;
var
n, i: integer;
l, a: real;
begin
write(taskВведи N > task);
readln(n);
a := 10; l := a;
for i := 2 to n do
begin
a := a * 1.1;
l := l + a
end;
writeln(l, task километров пробежит за task, n, task дней task)
end.
2.
program task_2;
var
n, i: integer;
begin
write(taskN > task);
readln(n);
for i := 1 to 10 do
writeln(n, task*task, i:2, task=task, n * i:3, n:6, task+task, i:2, task=task, n + i:3)
end.
3.
program task_3;
const
parol = 1234;
var
n, i: integer;
begin
write(taskВведи пароль (четырехзначное число > task);
readln(n);
repeat
writeln(taskНеправильно! Попробуй еще раз.task);
write(taskВведи пароль > task);
readln(n);
until n = parol;
writeln(taskВерно! Молодец!task)
end.
4.
program task_4;
var
a, i: integer;
b, s: real;
begin
write(taskСтипендия > task);
readln(a);
write(taskРасходы > task);
readln(b);
s := b;
for i := 2 to 10 do
begin
b := b * 1.03;
s := s + b
end;
writeln(taskРодительский взнос > task, (s - a * 10):6:2, taskруб.task)
end.
5.
program task_5;
var
n, i: integer;
begin
write(taskN > task);
readln(n);
for i := 1 to n do
if n mod i = 0 then
write(i, task task);
end.
6.
program task_6;
var
n, i, fac: integer;
begin
write(taskN > task);
readln(n);
if n = 0 then fac := 1
else
begin
fac := 1;
for i := 2 to n do
fac := fac * i
end;
writeln(taskФакториал task, n, task=task, fac);
end.
3 уровень сложности
1. Дано натуральное число N. Вычислить сумму ряда:
S=1!+2!+3!+…+N! (N > 1)
Протестировать программу для N=3 и N=5
2. Покупатель должен заплатить в кассу S рублей. У него имеются монеты в 1, 2 и 5 рублей, а также купюры достоинством в 10, 50, 100 и 500 рублей (достаточное количество). Сколько монет и купюр разного достоинства отдаст покупатель, если он начинает платить с самых крупных? Операции целочисленного деления (div и mod) использовать нельзя. Протестировать программу для S=567, S=1025, S=64, S=13.
3. Числа Фибоначчи (fn) определяются формулами:
f0=f1=1, fn=fn-1+fn-2 при n=2,3,…
Определить f10, f25, f40.
4. Вывести на экран все простые числа в диапазоне от 2 до N. Протестировать программу для N=100, N=300.
5. Даны натуральное N и действительное x. Вычислить сумму ряда:
sin x+sin x2+sin x3+…+sin xN
Протестировать программу для а) x=0.5, N=3, б) x=1, N=5. Проверить правильность её работы с помощью калькулятора.
6. Построить таблицу истинности для логического выражения (A OR B) AND C.
1.
program task_1;
var
n, i, fac, s, j: integer;
begin
write(taskN > task);
readln(n);
s := 0;
for i := 1 to n do
begin
fac := 1;
for j := 1 to i do
fac := fac * j;
//write(fac, task task);
s := s + fac
end;
writeln(taskСумма факториалов task, n, task=task, s);
end.
2.
program task_2;
var
s, k10, k50, k100, k500, m1, m2, m5: integer;
begin
write(taskS > task);
readln(s);
k10 := 0;k50 := 0;k100 := 0;
m1 := 0; m2 := 0;m5 := 0;
while s - 500 > =0 do
begin
k500 := k500 + 1;
s := s - 500
end;
while s - 100 > =0 do
begin
k100 := k100 + 1;
s := s - 100
end;
while s - 50 > =0 do
begin
k50 := k50 + 1;
s := s - 50
end;
while s - 10 > =0 do
begin
k10 := k10 + 1;
s := s - 10
end;
while s - 5 > = 0 do
begin
m5 := m5 + 1;
s := s - 5
end;
while s - 2 > =0 do
begin
m2 := m2 + 1;
s := s - 2
end;
m1 := s;
writeln(task500 купюр task, k500, task штукtask);
writeln(task100 купюр task, k100, task штукtask);
writeln(task50 купюр task, k50, task штукtask);
writeln(task10 купюр task, k10, task штукtask);
writeln(task5 монет task, m5, task штукtask);
writeln(task2 монет task, m2, task штукtask);
writeln(task1 монет task, m1, task штукtask);
end.
3.
program task_3;
var
n, f, f1, f2: longint;
i: byte;
begin
write(taskВведи n > task);
readln(n);
if (n = 0) or (n = 1) then f := 1
else
begin
f1 := 1; f2 := 1;
for i := 2 to n do
begin
f := f1 + f2;
f1 := f2; f2 := f;
//write(f, task task)
end;
end;
writeln(taskftask,n,task =task,f)
end.
n f
10 89
25 121393
40 165580141
4.
program task_4;
var
n, i, j: integer;
f: boolean;
begin
writeln(taskn > task);
readln(n);
for i := 2 to n do
begin
f := true;
for j := 2 to i - 1 do
if i mod j = 0 then begin f := false; break end;
if f then write(i, task task)
end;
end.
5.
program task_5;
var
n, i: integer;
x, a, s: real;
begin
write(taskN, x > task);
readln(n, x);
s := 0; a := x;
for i := 1 to n do
begin
s := s + sin(x);
x := x * a
end;
writeln(taskSum=task, s:5:2)
end.
6.
program task_6;
var
a, b, c, f: boolean;
begin
writeln(taskAtask:7, taskBtask:7, taskCtask:7, taskFtask:7);
for a := false to true do
for b := false to true do
for c := false to true do
begin
f := (a or b) and c;
write(a:7, b:7, c:7, f:7);
writeln
end;
end.
Практическое задание №25
Тема: Программирование циклов и ветвлений на Паскале.
Алгоритм Евклида
1 уровень сложности
1. Набрать и отладить программу нахождения наибольшего общего делителя и протестировать её на следующих исходных данных:
а) a=40 b=64
б) a=32 b=16
в) a=12 b=20
г) a=5 b=12
2. Составить на языке Паскаль программу, которая запрашивает с клавиатуры N целых чисел и считает, сколько из них положительных, сколько отрицательных и сколько нулей. Разработать для программы не менее двух тестов и доказать правильность её работы.
3. Написать программу, которая выводит на экран все двухзначные числа, делящиеся на 3 или на 5 (использовать операции целочисленного деления div или mod).
1.
program task_1;
var
M, N: integer;
begin
write(taskВведи M и N > > task);
readln(M, N);
while M N do
if M > N then M := M - N
else N := N - M;
writeln(taskНОД=task, M)
end.
2.
program task_2;
var
i, a, k1, k2, k0, n: integer;
begin
k1 := 0; k2 := 0;k0 := 0;
write(taskВведи количество чиселtask);
readln(n);
for i := 1 to n do
begin
write(taskВведи число:task);
readln(a);
if a > 0 then k1 := k1 + 1
else if a
else k0 := k0 + 1
end;
writeln(taskПоложительных > > task, k1, task Отрицательных > > task, k2, task Количество нулей > > task, k0)
end.
3.
program task_3;
var
i: integer;
begin
for i := 10 to 99 do
if (i mod 3 = 0) or (i mod 5 = 0) then write(i, task task)
end.
2 уровень сложности
1. Составить программу нахождения наименьшего общего кратного (НОК) двух чисел m и n, используя формулу n*m=НОД(n,m)*НОК(n,m). Разработать тесты для проверки правильности работы программы.
2. Проверить, являются ли два числа a и b взаимно простыми. Два числа называются взаимно простыми, если их наибольший общий делитель равен 1. Протестировать программу для следующих исходных данных:
а) a=5 b=95
б) a=3 b=100
в) a=11 b=98
3. Написать программу сокращения дроби , где N – целое, M – натуральное число. Использовать алгоритм Евклида. Разработать тесты для проверки правильности работы программы.
1.
program task_1;
var
m, n, p, d: integer;
begin
write(taskВведи M, N > > task);
readln(m, n);
p := m * n;
while m n do //определение НОД
if m > n then m := m - n
else n := n - m;
d := m;//НОД
writeln(taskНОK =task, p div d)
end.
1) 10, 30
2) 40, 16
3) 15, 80
2.
program task_2;
var
a, b: integer;
begin
write(taskВведи a и b > > task);
readln(a, b);
while a b do
if a > b then a := a - b
else b := b - a;
if a = 1 then writeln(taskЧисла взаимно простыеtask)
else writeln(taskЧисла не взаимно простыеtask);
end.
3.
program task_3;
var
M, N, a, b, c: integer;
begin
write(taskВведи M и N > > task);
readln(M, N);
a := M; b := N;
while M N do
if M > N then M := M - N
else N := N - M;
c := M;
writeln(taskСокращенная дробь > task, a / c, task/task, b / c)
end.
1) 5 15
2) 24 4
3) 21 43
3 уровень сложности
1. Составить на языке Паскаль программу нахождения наибольшего общего делителя трёх чисел, используя следующую формулу: НОД(a,b,c)=НОД(НОД(a,b),c). Протестировать программу на следующих исходных данных:
а) a=40 b=64 c=120
б) a=32 b=45 c=60
в) a=11 b=220 c=33
г) a=175 b=1025 c=600
2. Написать программу, запрашивающую с клавиатуры целые числа и определяющую максимальное и минимальное из них. Окончание ввода – число 0. Протестировать программу для последовательности: -3 5 6 -11 24 -1 0.
3. Составить программу для графического изображения делимости чисел от 1 до N (N – исходное данное). В каждой строке надо выводить число и столько плюсов, сколько делителей у этого числа. Например, если исходное данное число равно 4, то на экране должно быть выведено:
1+
2++
3++
4+++
1.
program task_1;
var
a, b, c, d: integer;
begin
write(taskВведи a, b, c > > task);
readln(a, b, c);
while a b do
if a > b then a := a - b
else b := b - a;
d := a;//НОД a, b
while d c do
if d > c then d := d - c
else c := c - d;
writeln(taskНОД =task, d)//НОД a, b, c
end.
2.
program task_2;
var
a, max, min: integer;
begin
write(taskВведи число > > task);
readln(a);
max := a; min := a;
while a 0 do
begin
if a > max then max := a;
if a
write(taskВведи число > > task);
readln(a);
end;
writeln(taskmax=task, max, task min=task, min)
end.
3.
program task_3;
var
n, j, i: integer;
begin
writeln(taskвведите числоtask);
readln(n);
for i := 1 to n do
begin
write(i);
for j := 1 to n do
if (i mod j = 0) then
write(task+task);
writeln;
end;
end.
ЕК ЦОР: Часть2, глава 6, §39. ЦОР № 16
Программа-конструктор






