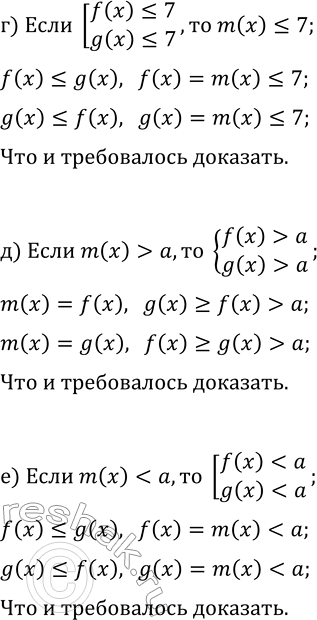Дополнительная задача 6 Глава 2 ГДЗ Мордкович Семенов 9 класс (Алгебра)
6. Докажите, что: а) всякое решение неравенства m(x) > =0 является решением системы {f(x) > =0, g(x) > =0}; б) наоборот, всякое решение системы {f(x) >
Ниже вариант решения задания из учебника Мордкович, Семенов, Александрова 9 класс, Бином:
6. Докажите, что:
а) всякое решение неравенства m(x) > =0 является решением системы {f(x) > =0, g(x) > =0};
б) наоборот, всякое решение системы {f(x) > =0, g(x) > =0} является решением неравенства m(x) > =0;
в) всякое решение неравенства m(x)
г) наоборот, всякое решение совокупности [f(x)
д) неравенство m(x) > a и система {f(x) > a, g(x) > a} равносильны, т. е. имеют одинаковые множества решений;
е) неравенство m(x)
На координатной плоскости изобразите множество решений данной системы уравнений или неравенств.