4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс

Упражнение 278 Повторение ГДЗ Мерзляк 11 класс Базовый уровень (Алгебра)

278. Является ли чётной либо нечётной функция: 1) f(x)=6x^3-7x^5; 5) f(x)=1/(x^3-2x); 2) f(x)=(x^2+4)/(x^2-1); 6) f(x)=(x+5)(x-1)-4x; 3) f(x)=√(6-x^2); 7) f(x)=(x-6)^2-(x+6)^2; 4) f(x)=x^2+x-3;


Решебник Мерзляк Алгебра

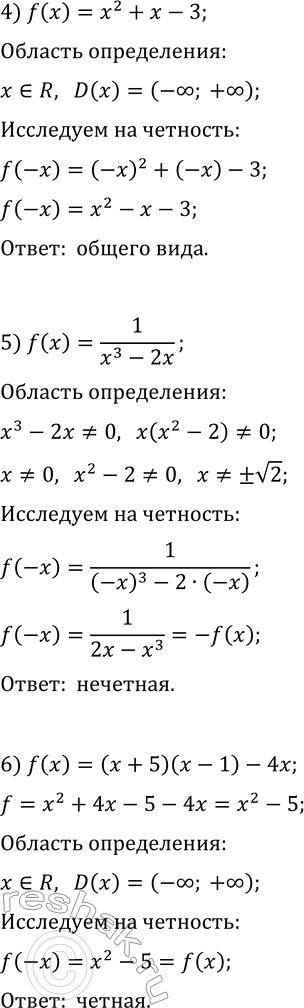
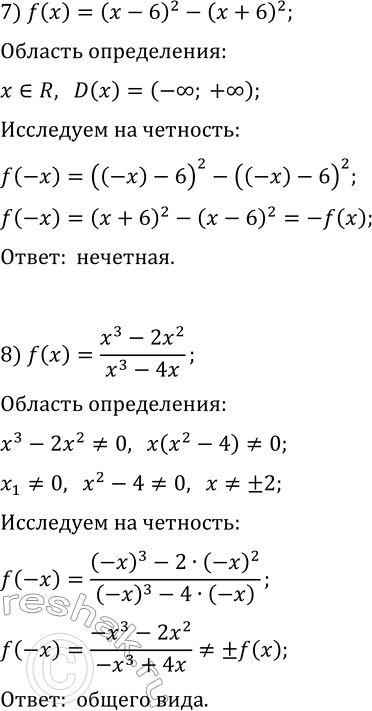
Решение задачи: 278. Является ли чётной либо нечётной функция: 1) f(x)=6x^3-7x^5; 5) f(x)=1/(x^3-2x); 2) f(x)=(x^2+4)/(x^2-1); 6) f(x)=(x+5)(x-1)-4x; 3) f(x)=в€љ(6-x^2); 7) f(x)=(x-6)^2-(x+6)^2; 4) f(x)=x^2+x-3;Решение задачи: 278. Является ли чётной либо нечётной функция: 1) f(x)=6x^3-7x^5; 5) f(x)=1/(x^3-2x); 2) f(x)=(x^2+4)/(x^2-1); 6) f(x)=(x+5)(x-1)-4x; 3) f(x)=в€љ(6-x^2); 7) f(x)=(x-6)^2-(x+6)^2; 4) f(x)=x^2+x-3;Решение задачи: 278. Является ли чётной либо нечётной функция: 1) f(x)=6x^3-7x^5; 5) f(x)=1/(x^3-2x); 2) f(x)=(x^2+4)/(x^2-1); 6) f(x)=(x+5)(x-1)-4x; 3) f(x)=в€љ(6-x^2); 7) f(x)=(x-6)^2-(x+6)^2; 4) f(x)=x^2+x-3;
Решебник Мерзляк Алгебра
Навигация по заданиям
…273274275276277278279280281282283…

Ниже вариант решения задания из учебника Мерзляк, Номировский, Полонский 11 класс, Просвещение:

278. Является ли чётной либо нечётной функция:

1) f(x)=6x^3-7x^5; 5) f(x)=1/(x^3-2x);

2) f(x)=(x^2+4)/(x^2-1); 6) f(x)=(x+5)(x-1)-4x;

3) f(x)=в€љ(6-x^2); 7) f(x)=(x-6)^2-(x+6)^2;

4) f(x)=x^2+x-3; 8) f(x)=(x^3-2x^2)/(x^3-4x)?