Задание 3 Параграф 20 ГДЗ Семакин 11 класс (Информатика)
3. а) Сформулируйте задачу оптимального планирования для школьного кондитерского цеха, в котором выпускается три вида продукции: пирожки, пирожные и коржики. Предполагаются все условия, которые оговорены в примере учебника:


Ниже вариант решения задания из учебника Семакин, Хеннер, Шеина 11 класс, Просвещение:
3. а) Сформулируйте задачу оптимального планирования для школьного кондитерского цеха, в котором выпускается три вида продукции: пирожки, пирожные и коржики.
Предполагаются все условия, которые оговорены в примере учебника:
- приготовить можно только 700 штук изделий;
- рабочий день 8 часов;
- только пирожков за день можно произвести 1000 штук;
- только пирожных за день можно произвести 250 штук;
- дополнительно к заданию для трех изделий: только коржиков за день можно произвести 500 штук;
x – дневной план выпуска пирожков;
y – дневной план выпуска пирожных;
z – дневной план выпуска коржиков.
Суммарное время на изготовления трех изделий:
xt + 4ty + 2tz=t(x + 4y + 2z)
Это время не может быть больше 8 часов
t(x + 4y + 2z)
Так как t это время изготовления одного пирожка, и за день можно изготовить только пирожков 1000, то t = 480/1000=0,48
Подставив эту величину в уравнение, и преобразовав получаем:
x + 4y + 2z
Всего изделия может быть изготовлено не более 700, т.е.
x + y + z
Если учесть, что количества изделий не может быть отрицательно, то:
x > =0; y > =0; z > =0
Математическая модель этой задачи оптимального планирования – это система следующих неравенств:
x + 4y + 2z
x + y + z
x > =0; y > =0; z > =0.
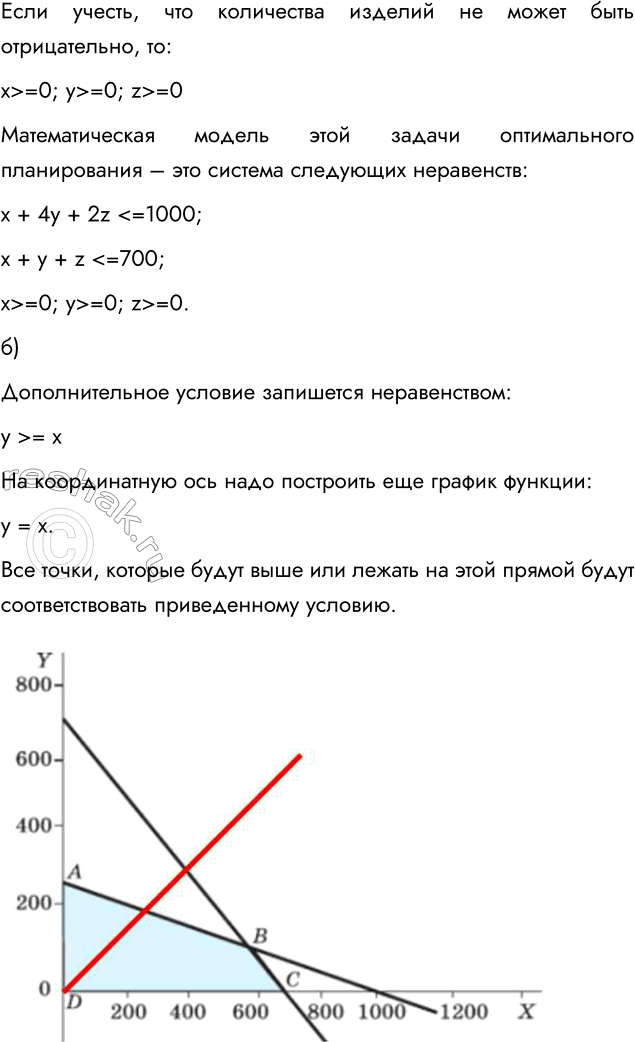
б) Внесите изменение в постановку задачи оптимального планирования из этого параграфа для двух видов продукции с учетом еще одного ограничения: число пирожных должно быть не меньше числа пирожков. На координатной плоскости постройте область поиска решения.
Дополнительное условие запишется неравенством:
y > = x
На координатную ось надо построить еще график функции:
y = x.
Все точки, которые будут выше или лежать на этой прямой будут соответствовать приведенному условию.
Решением будет та точка, где целевая функция максимальна. Воспользуемся поиском решений с использованием Excel
Надо использовать целевую функцию. Она представлена в примере:
f(x,y)=x+2y
Результаты поиска решений представлены ниже.
Согласно этим результатам, оптимальное решение на графике будет соответствовать точке х=200, у=200.
Другие возможные результаты (не оптимальные) в закрашенной области выше красной линии.
Пример: Z_Г3.xlsx Лист 4






