4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс

Задания Кто хочет знать больше ГДЗ Мерзляк 11 класс Базовый уровень (Алгебра)

1. Пусть D(x) — дисперсия случайной величины х. Докажите, что D(x)=M(x^2)-(M(x))^2. 2. Пусть D(х) — дисперсия случайной величины х и с — константа.


Решебник Мерзляк Алгебра

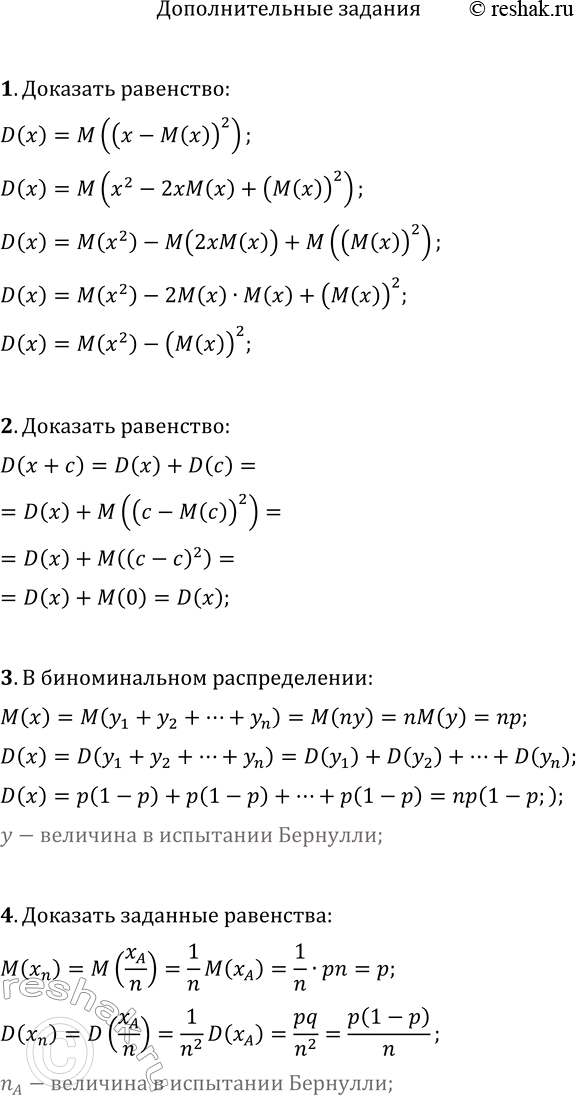
Решение задачи: 1. Пусть D(x) — дисперсия случайной величины х. Докажите, что D(x)=M(x^2)-(M(x))^2. 2. Пусть D(х) — дисперсия случайной величины х и с — константа.Решение задачи: 1. Пусть D(x) — дисперсия случайной величины х. Докажите, что D(x)=M(x^2)-(M(x))^2. 2. Пусть D(х) — дисперсия случайной величины х и с — константа.Решение задачи: 1. Пусть D(x) — дисперсия случайной величины х. Докажите, что D(x)=M(x^2)-(M(x))^2. 2. Пусть D(х) — дисперсия случайной величины х и с — константа.Решение задачи: 1. Пусть D(x) — дисперсия случайной величины х. Докажите, что D(x)=M(x^2)-(M(x))^2. 2. Пусть D(х) — дисперсия случайной величины х и с — константа.Решение задачи: 1. Пусть D(x) — дисперсия случайной величины х. Докажите, что D(x)=M(x^2)-(M(x))^2. 2. Пусть D(х) — дисперсия случайной величины х и с — константа.
Решебник Мерзляк Алгебра
Навигация по заданиям
…20.2020.2120.2220.2320.24Кто хочет знать больше12345…

Ниже вариант решения задания из учебника Мерзляк, Номировский, Полонский 11 класс, Просвещение:

1. Пусть D(x) — дисперсия случайной величины х. Докажите, что D(x)=M(x^2)-(M(x))^2.

2. Пусть D(х) — дисперсия случайной величины х и с — константа. Докажите, что D(x+c)=D(x).

3. Пусть случайная величинах x имеет биномиальное распределение с параметрами n и p. Докажите, что M(x)=np, D(x)=np(1-p).

4. Вероятность события А в некотором испытании равна р. Проводят серию из n таких испытаний и подсчитывают частоту x_n=x_A/n события А. где n_A — число испытаний в этой серии, в которых произошло событие A. Докажите, что M(x_n)=p, D(x_n)=p(1-p)/n.

1. Монету подбрасывают дважды. Случайная величина х равна количеству выпавших при этом гербов. Найдите:

1) распределение случайной величины х;

2) распределение случайной величины x^2:

3) распределение случайной величины z=x+x^2.

2. Монету и кубик подбрасывают одновременно. Случайная величинах равна числу, выпавшему на кубике, а случайная величина у равна 1, если монета выпала кверху гербом, и 0, если числом. Найдите:

1) распределение случайной величины х;

2) распределение случайной величины у;

3) распределение случайной величины z=xy.

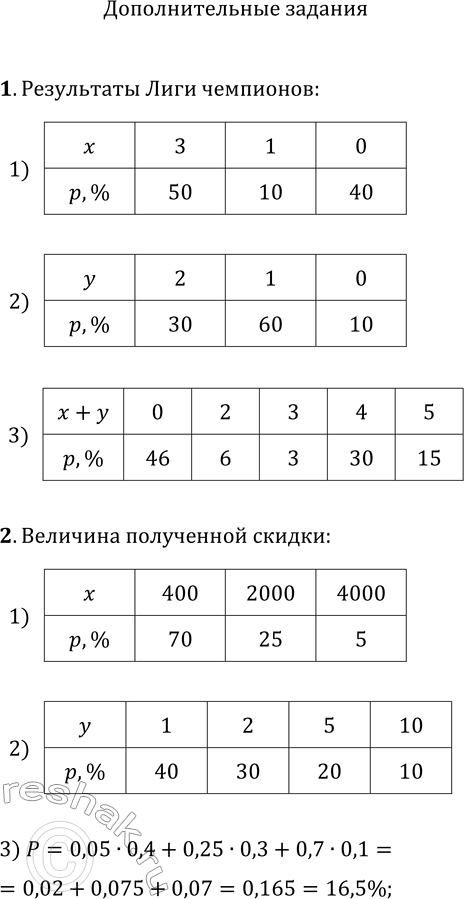
1. В условиях задачи о турнире Лиги чемпионов найдите распределение суммы случайных величин x и у.

2. Туристическая фирма проводит акцию «Выбери цену сам!». Клиенту, планирующему купить путёвку, предлагается независимо вытянуть два билета: первый — с величиной ежедневной скидки за путевку, второй — с количеством дней, в течение которых будет действовать эта скидка. Найдите вероятность того, что туристическая фирма предоставит клиенту скидку на общую сумму 4000 р.

1. Найдите дисперсии случайных величин х и у, рассмотренных в примере о безопасности автомобиля.

2. Найдите дисперсию числа очков, выпадающих при бросании игрального кубика.

3. Пусть случайная величина x имеет распределение Бернулли:

Докажите, что M(x)=p, D(x)=p(1-p).

1. О случайной величине х известно, что M(x)=5, D(x)=3. Найдите математическое ожидание и дисперсию случайной величины:

1) y=2x; 2) z=-x; 3) t=x/3.

2. На карте с масштабом 1 : 10 000 линейкой измеряют расстояние между точками А и В. Случайная величина х равна измеренному расстоянию (в сантиметрах). Известно, что M(x)=7, D(x)=0,1. Оцените расстояние на местности между пунктами A и В (в метрах). Чему равна дисперсия величины, равной вычисленному расстоянию между пунктами A и В на местности?