Упражнение 29.10 ГДЗ Мордкович Семенов 9 класс (Алгебра)
29.10. Докажите, что если числа 1/a, 1/b, 1/c в заданном порядке образуют конечную арифметическую прогрессию, то верно равенство: а) ab+bc+ac=3ac; б) b/c+b/a=2.
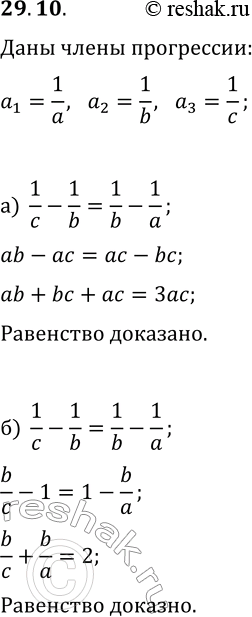
Ниже вариант решения задания из учебника Мордкович, Семенов, Александрова 9 класс, Бином:
29.10. Докажите, что если числа 1/a, 1/b, 1/c в заданном порядке образуют конечную арифметическую прогрессию, то верно равенство:
а) ab+bc+ac=3ac; б) b/c+b/a=2.
