4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс

Упражнение 13.3 ГДЗ Мерзляк 11 класс Базовый уровень (Алгебра)

13.3. Докажите, что при любом натуральном n выполняется равенство: 1) 1+2+3+...+n=n(n+1)/2; 2) 1^3+2^3+3^3+...+n^3=(n(n+1)/2)^2; 3) 1^2+2^2+3^2+...+n^2=n(n+1)(2n+1)/6; 4) 1^2+3^2+5^2+...+(2n-1)^2=n(4n^2-1)/3. *Цитирирование задания со ссылкой на учебник производится исключительно в учебных целях для лучшего понимания разбора решения задания.


Решебник Мерзляк Алгебра

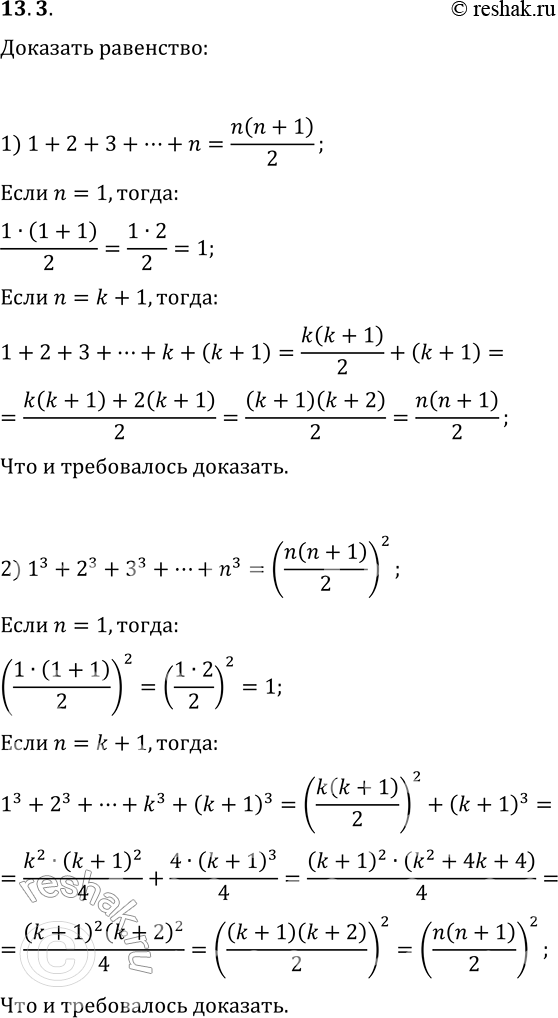
Решение задачи: 13.3. Докажите, что при любом натуральном n выполняется равенство: 1) 1+2+3+...+n=n(n+1)/2; 2) 1^3+2^3+3^3+...+n^3=(n(n+1)/2)^2; 3) 1^2+2^2+3^2+...+n^2=n(n+1)(2n+1)/6; 4) 1^2+3^2+5^2+...+(2n-1)^2=n(4n^2-1)/3. *Цитирирование задания со ссылкой на учебник производится исключительно в учебных целях для лучшего понимания разбора решения задания.Решение задачи: 13.3. Докажите, что при любом натуральном n выполняется равенство: 1) 1+2+3+...+n=n(n+1)/2; 2) 1^3+2^3+3^3+...+n^3=(n(n+1)/2)^2; 3) 1^2+2^2+3^2+...+n^2=n(n+1)(2n+1)/6; 4) 1^2+3^2+5^2+...+(2n-1)^2=n(4n^2-1)/3. *Цитирирование задания со ссылкой на учебник производится исключительно в учебных целях для лучшего понимания разбора решения задания.
Решебник Мерзляк Алгебра
Навигация по заданиям
…12.712.8Вопросы13.113.213.313.413.513.613.713.8…

Ниже вариант решения задания из учебника Мерзляк, Номировский, Полонский 11 класс, Просвещение:

13.3. Докажите, что при любом натуральном n выполняется равенство:

1) 1+2+3+...+n=n(n+1)/2;

2) 1^3+2^3+3^3+...+n^3=(n(n+1)/2)^2;

3) 1^2+2^2+3^2+...+n^2=n(n+1)(2n+1)/6;

4) 1^2+3^2+5^2+...+(2n-1)^2=n(4n^2-1)/3.