Упражнение 164 ГДЗ Колягин Ткачёва 7 класс (Алгебра)
С помощью контрпримера опровергнуть высказывание: 1) модуль любого целого числа — число натуральное; 2) если а 3) для любого х имеем |-x| = х;

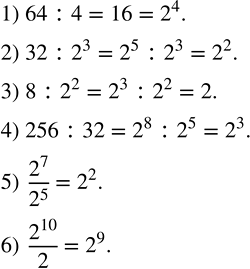
Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:
С помощью контрпримера опровергнуть высказывание:
1) модуль любого целого числа — число натуральное;
2) если а
3) для любого х имеем |-x| = х;
4) для любых а и b имеем |а + b| = |а| + |b|;
5) для любого х число -х — отрицательное;
6) если а
Записать в виде степени с основанием 2:
1) 64:4; 2) 32:2^3; 3) 8:2^2; 4) 256:32; 5) 2^7/2^5 ; 6) 2^10/2.






