Упражнение 535 ГДЗ Колягин Ткачёва 7 класс (Алгебра)

Доказать, что число (7n+1)^2-(2n-4)^2 делится на 15 при любом натуральном n.Квадрат со стороной 4 расположен так, что центр его находится в начале координат, а стороны параллельны осям координат.

Решение задачи: Доказать, что число (7n+1)^2-(2n-4)^2 делится на 15 при любом натуральном n.Квадрат со стороной 4 расположен так, что центр его находится в начале координат, а стороны параллельны осям координат.

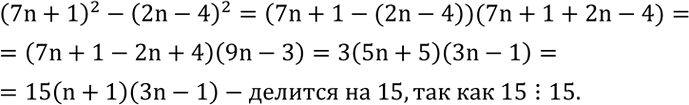
Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:

Доказать, что число (7n+1)^2-(2n-4)^2 делится на 15 при любом натуральном n.

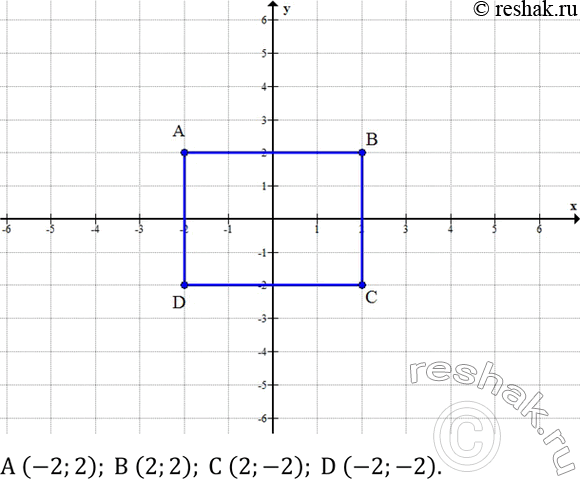
Квадрат со стороной 4 расположен так, что центр его находится в начале координат, а стороны параллельны осям координат. Найти координаты вершин квадрата.