Упражнение 419 ГДЗ Колягин Ткачёва 7 класс (Алгебра)
Упростить: 1) 12,5x^2+y^2-(8x^2-5y^2-(-10x^2+(5,5x^2-6y^2 ))); 2) 0,6ab^2+(2a^3+b^3-(3ab^2-(a^3+2,4ab^2-b^3 ))). Скорость пассажирского поезда равна 60 км/ч, а товарного - 40 км/ч. Найти расстояние между двумя пунктами, если пассажирский поезд проходит это расстояние на 2 ч быстрее, чем товарный.
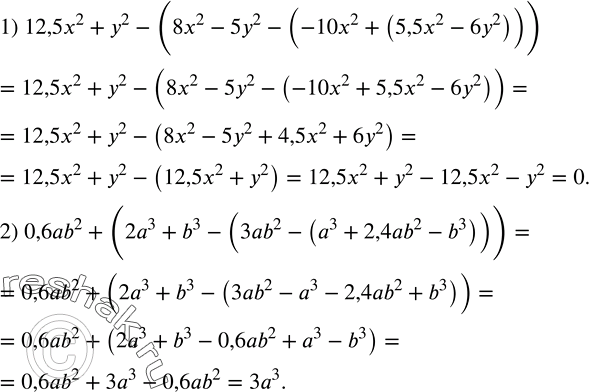

Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:
Упростить:
1) 12,5x^2+y^2-(8x^2-5y^2-(-10x^2+(5,5x^2-6y^2 )));
2) 0,6ab^2+(2a^3+b^3-(3ab^2-(a^3+2,4ab^2-b^3 ))).
Скорость пассажирского поезда равна 60 км/ч, а товарного - 40 км/ч. Найти расстояние между двумя пунктами, если пассажирский поезд проходит это расстояние на 2 ч быстрее, чем товарный.
