Упражнение 848 ГДЗ Колягин Ткачёва 7 класс (Алгебра)
Доказать, что если x, y, z положительны, то равенство x^3+y^3+z^3=3xyz является верным только тогда, когда x=y=z. *Цитирирование задания со ссылкой на учебник производится исключительно в учебных целях для лучшего понимания разбора решения задания.
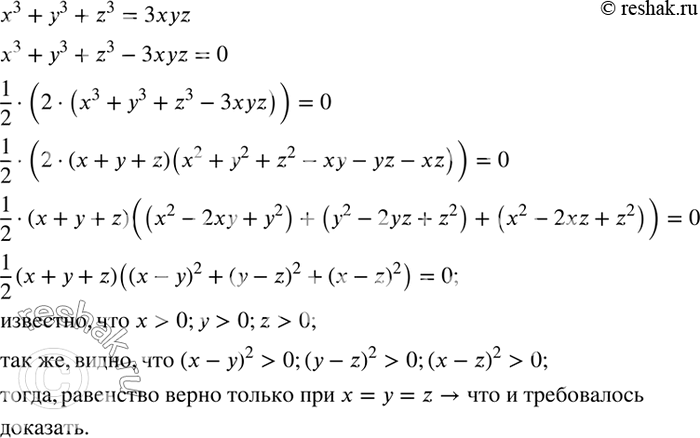
Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:
Доказать, что если x, y, z положительны, то равенство x^3+y^3+z^3=3xyz является верным только тогда, когда x=y=z.
