4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс

Упражнение 19.9 ГДЗ Мордкович Семенов 9 класс (Алгебра)

19.9. Используя свойства числовых неравенств, докажите, что данная функция убывает: а) y=-2x^3-x; г) y=-3x^3-2x; б) y=x^6-3x, x?0; д) y=-2x^6-5x, x?0; в) y=(x+9)/(x+3), x >


Решебник Мордкович Алгебра

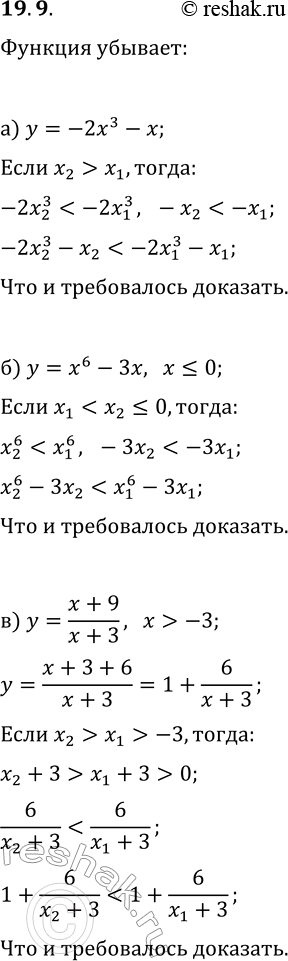
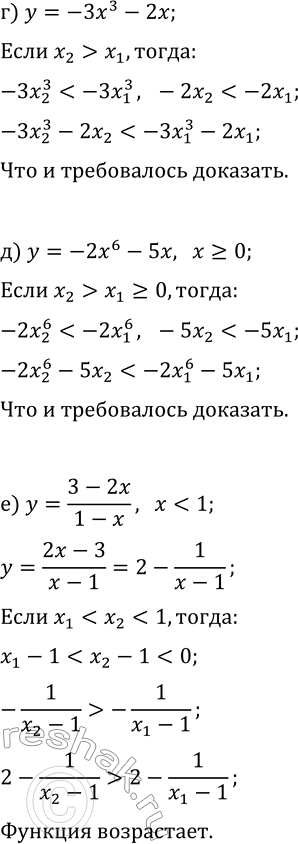
Решение задачи: 19.9. Используя свойства числовых неравенств, докажите, что данная функция убывает: а) y=-2x^3-x; г) y=-3x^3-2x; б) y=x^6-3x, x?0; д) y=-2x^6-5x, x?0; в) y=(x+9)/(x+3), x >Решение задачи: 19.9. Используя свойства числовых неравенств, докажите, что данная функция убывает: а) y=-2x^3-x; г) y=-3x^3-2x; б) y=x^6-3x, x?0; д) y=-2x^6-5x, x?0; в) y=(x+9)/(x+3), x >
Решебник Мордкович Алгебра
Навигация по заданиям
…19.419.519.619.719.819.919.1019.1119.1219.1319.14…

Ниже вариант решения задания из учебника Мордкович, Семенов, Александрова 9 класс, Бином:

19.9. Используя свойства числовых неравенств, докажите, что данная функция убывает:

а) y=-2x^3-x; г) y=-3x^3-2x;

б) y=x^6-3x, x?0; д) y=-2x^6-5x, x?0;

в) y=(x+9)/(x+3), x > -3; е) y=(3-2x)/(1-x), x