Упражнение 425 ГДЗ Колягин Ткачёва 7 класс (Алгебра)

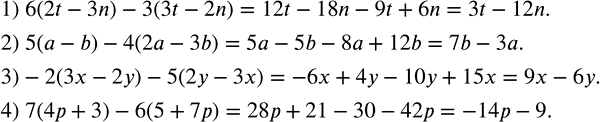
Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:

Упростить выражение:

1) 6(2t-3n)-3(3t-2n);

2) 5(a-b)-4(2a-3b);

3) -2(3x-2y)-5(2y-3x);

4) 7(4p+3)-6(5+7p).

1) Доказать, что если сумма трех последовательных натуральных чисел есть число нечетное, то их произведение делится на 24.

2) Доказать, что если сумма четырех натуральных чисел есть число нечетное, то их произведение - число четное.