Упражнение 7.2 ГДЗ Мордкович Семенов 9 класс (Алгебра)

7.2. Решите систему уравнений методом введения новых переменных: а) {x^2-3y^2=-3, x^4-y^4=65}; г) {2x^2-3y^2=-10, x^4-y^4=-15}; б) {x^2+2y^2=17, x^4+2y^4=113}; д) {3x^2+y^2=28, 2x^4-y^4=161}; в) {(x+y)^2+2(x-y)^2=11, (x+y)^4-(x-y)^4=80};

$Решение задачи: 7.2. Решите систему уравнений методом введения новых переменных: а) {x^2-3y^2=-3, x^4-y^4=65}; г) {2x^2-3y^2=-10, x^4-y^4=-15}; б) {x^2+2y^2=17, x^4+2y^4=113}; д) {3x^2+y^2=28, 2x^4-y^4=161}; в) {(x+y)^2+2(x-y)^2=11, (x+y)^4-(x-y)^4=80};$ $Решение задачи: 7.2. Решите систему уравнений методом введения новых переменных: а) {x^2-3y^2=-3, x^4-y^4=65}; г) {2x^2-3y^2=-10, x^4-y^4=-15}; б) {x^2+2y^2=17, x^4+2y^4=113}; д) {3x^2+y^2=28, 2x^4-y^4=161}; в) {(x+y)^2+2(x-y)^2=11, (x+y)^4-(x-y)^4=80};$ $Решение задачи: 7.2. Решите систему уравнений методом введения новых переменных: а) {x^2-3y^2=-3, x^4-y^4=65}; г) {2x^2-3y^2=-10, x^4-y^4=-15}; б) {x^2+2y^2=17, x^4+2y^4=113}; д) {3x^2+y^2=28, 2x^4-y^4=161}; в) {(x+y)^2+2(x-y)^2=11, (x+y)^4-(x-y)^4=80};$ $Решение задачи: 7.2. Решите систему уравнений методом введения новых переменных: а) {x^2-3y^2=-3, x^4-y^4=65}; г) {2x^2-3y^2=-10, x^4-y^4=-15}; б) {x^2+2y^2=17, x^4+2y^4=113}; д) {3x^2+y^2=28, 2x^4-y^4=161}; в) {(x+y)^2+2(x-y)^2=11, (x+y)^4-(x-y)^4=80};$ $Решение задачи: 7.2. Решите систему уравнений методом введения новых переменных: а) {x^2-3y^2=-3, x^4-y^4=65}; г) {2x^2-3y^2=-10, x^4-y^4=-15}; б) {x^2+2y^2=17, x^4+2y^4=113}; д) {3x^2+y^2=28, 2x^4-y^4=161}; в) {(x+y)^2+2(x-y)^2=11, (x+y)^4-(x-y)^4=80};$

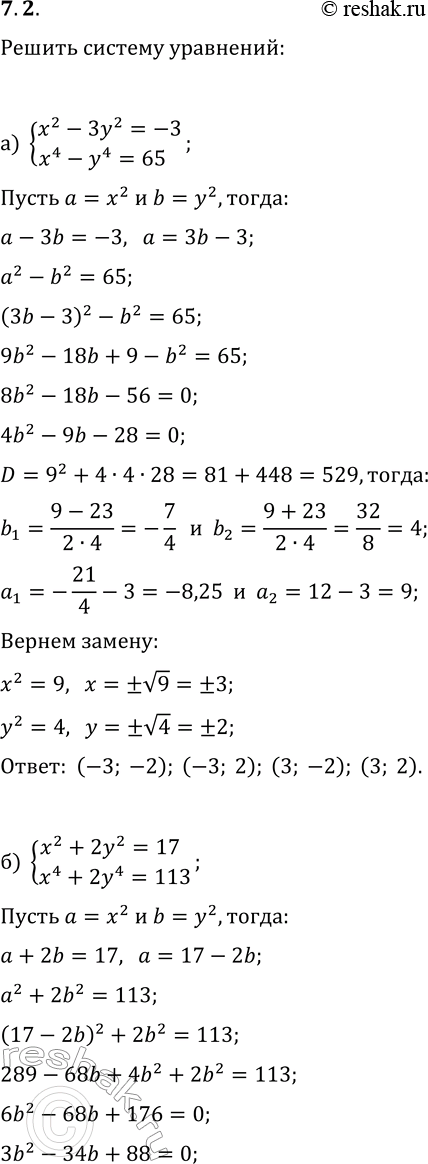
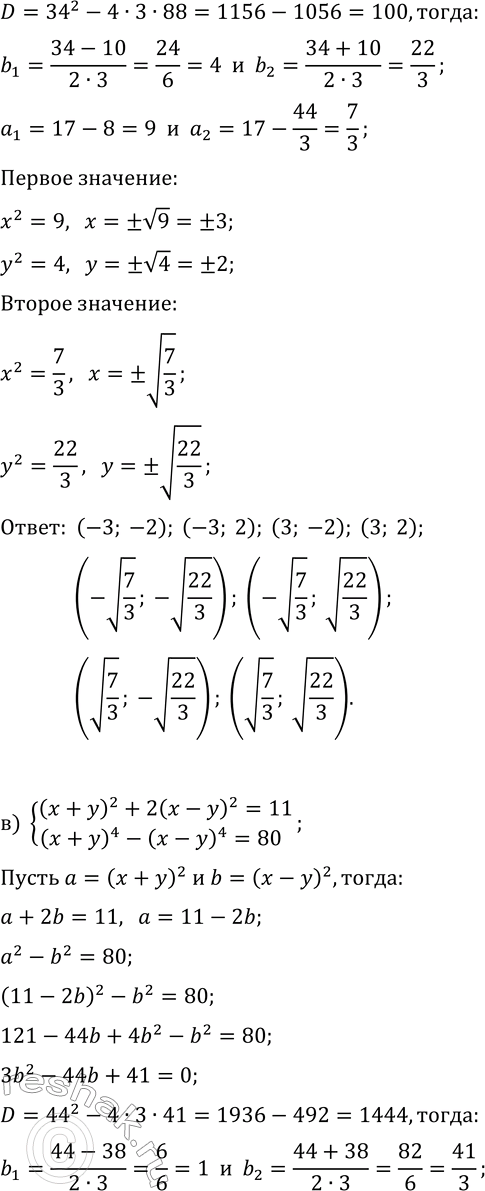
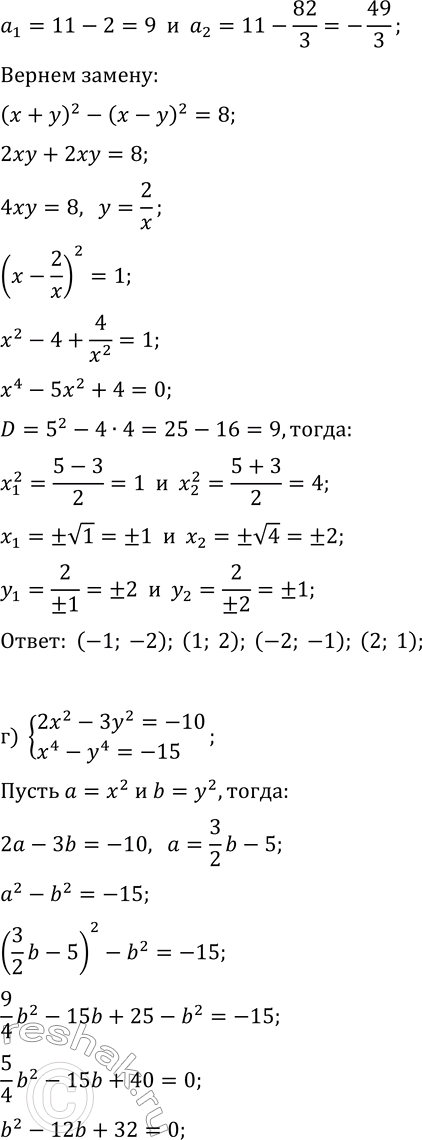
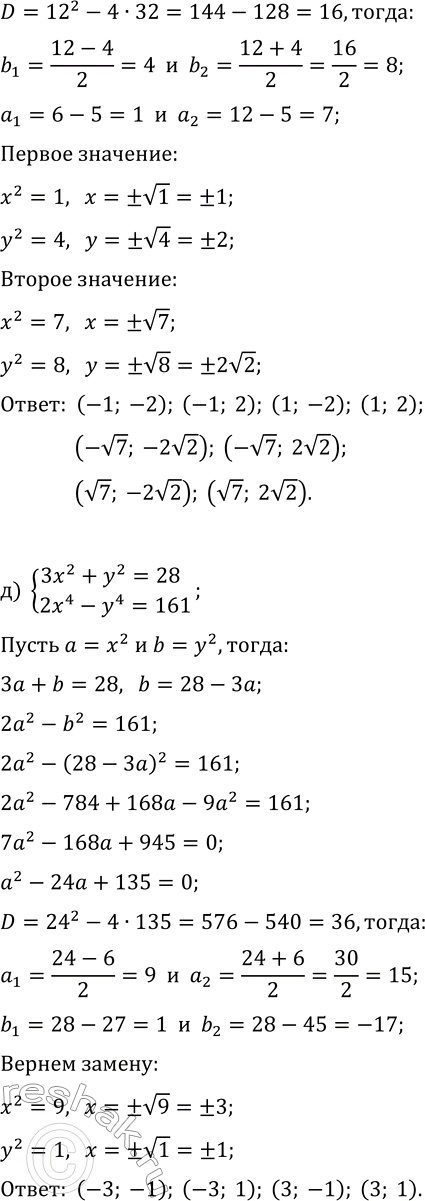
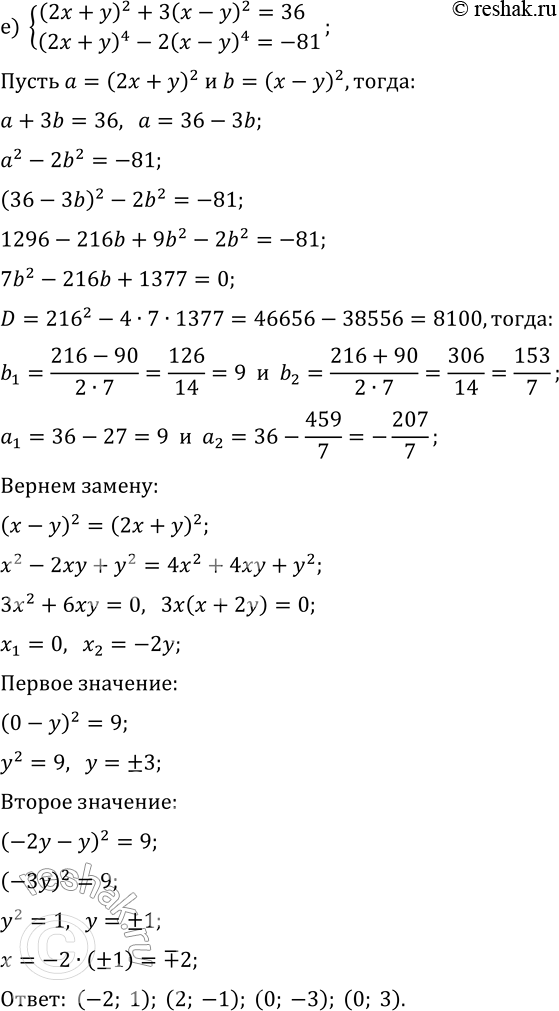
Ниже вариант решения задания из учебника Мордкович, Семенов, Александрова 9 класс, Бином:

7.2. Решите систему уравнений методом введения новых переменных:

а) {x^2-3y^2=-3, x^4-y^4=65}; г) {2x^2-3y^2=-10, x^4-y^4=-15};

б) {x^2+2y^2=17, x^4+2y^4=113}; д) {3x^2+y^2=28, 2x^4-y^4=161};

в) {(x+y)^2+2(x-y)^2=11, (x+y)^4-(x-y)^4=80};

е) {(2x+y)^2+3(x-y)^2=36, (2x+y)^4-2(x-y)^4=-81}.