4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс

Упражнение 5.12 ГДЗ Мерзляк 10 класс Углубленный уровень (Алгебра)

5.12. Докажите, что функция является чётной: 1) f(x)=-3x^2+|x|-1; 2) f(x)=x^3/(v(1-x)-v(x+1)); 3) f(x)=v(x^2-3x+5)+v(x^2+3x+5); 4) f(x)=(x+2)|x-4|-(x-2)|x+4|. *Цитирирование задания со ссылкой на учебник производится исключительно в учебных целях для лучшего понимания разбора решения задания.


Решебник Мерзляк (Углубленный) Алгебра

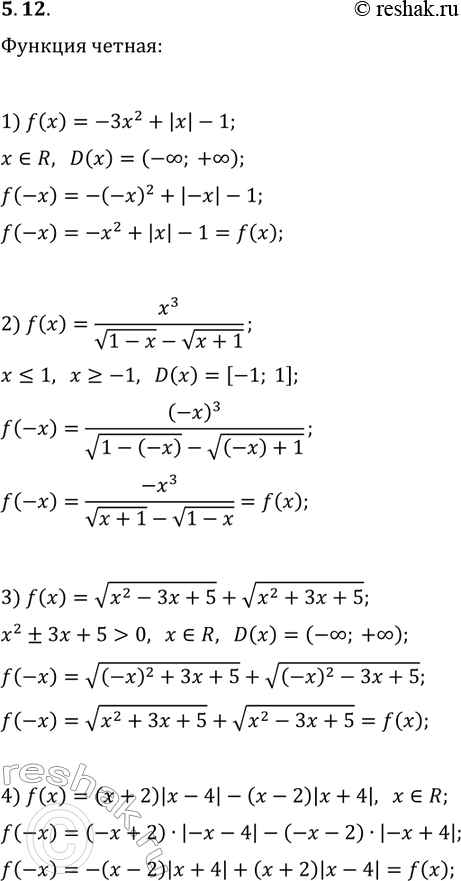
Решение задачи: 5.12. Докажите, что функция является чётной: 1) f(x)=-3x^2+|x|-1; 2) f(x)=x^3/(v(1-x)-v(x+1)); 3) f(x)=v(x^2-3x+5)+v(x^2+3x+5); 4) f(x)=(x+2)|x-4|-(x-2)|x+4|. *Цитирирование задания со ссылкой на учебник производится исключительно в учебных целях для лучшего понимания разбора решения задания.
Решебник Мерзляк (Углубленный) Алгебра
Навигация по заданиям
…5.75.85.95.105.115.125.135.145.155.165.17…

Ниже вариант решения задания из учебника Мерзляк, Номировский, Поляков 10 класс, Просвещение:

5.12. Докажите, что функция является чётной:

1) f(x)=-3x^2+|x|-1;

2) f(x)=x^3/(v(1-x)-v(x+1));

3) f(x)=v(x^2-3x+5)+v(x^2+3x+5);

4) f(x)=(x+2)|x-4|-(x-2)|x+4|.