Упражнение 367 ГДЗ Колягин Ткачёва 7 класс (Алгебра)

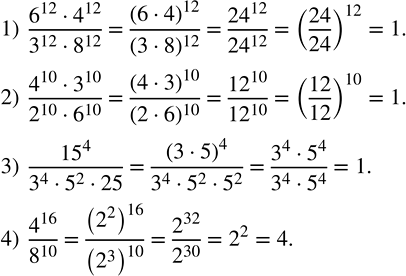
Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:

Вычислить:

1) (6^12•4^12)/(3^12•8^12 );

2) (4^10•3^10)/(2^10•6^10 );

3) ?15?^4/(3^4•5^2•25);

4) 4^16/8^10 .

Доказать, что разность квадратов любого натурального числа (больше 1) и числа, ему предществующего в ряду натуральных чисел, есть нечетное число.