Упражнение 363 ГДЗ Колягин Ткачёва 7 класс (Алгебра)

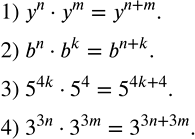
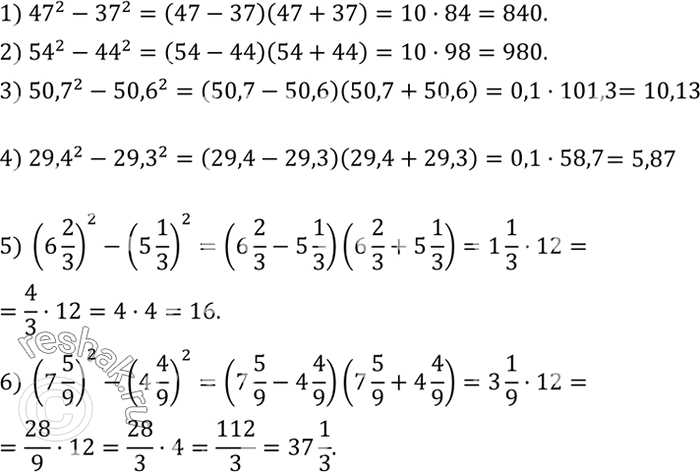
Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:

Пусть n, m, k - натуральные числа. Представить выражение в виде степени:

1) y^n•y^m;

2) b^n•b^k;

3) 5^4k•5^4;

4) 3^3n•3^3m.

Вычислить:

1) ?47?^2-?37?^2;

2) ?54?^2-?44?^2;

3) ?50,7?^2-?50,6?^2;

4) ?29,4?^2-?29,3?^2;

5) (6 2/3)^2-(5 1/3)^2;

6) (7 5/9)^2-(4 4/9)^2.