4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс

Упражнение 368 ГДЗ Колягин Ткачёва 7 класс (Алгебра)

Вычислить: 1) (35/48)^3•(6/7)^3•(1 3/5)^2; 2) (14/15)^4•(3/7)^4•(2,5)^3; 3) (5^3/6^2 )^4•(2/5)^5•(3/5)^7; 4) (7^4/?15?^2 )^3•(5/7)^6•(3/7)^5. Доказать, что число (7n+1)^2-(2n-4)^2 делится на 15 при любом натуральном n.


Решебник Колягин (2023) Алгебра

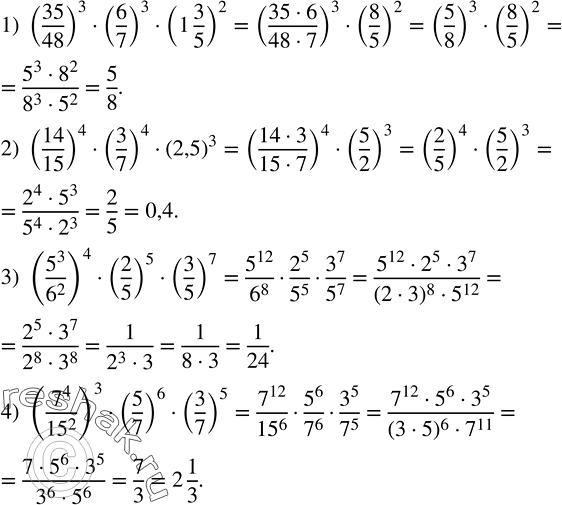
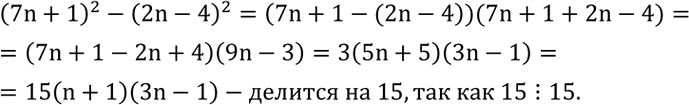
Решение задачи: Вычислить: 1) (35/48)^3•(6/7)^3•(1 3/5)^2; 2) (14/15)^4•(3/7)^4•(2,5)^3; 3) (5^3/6^2 )^4•(2/5)^5•(3/5)^7; 4) (7^4/?15?^2 )^3•(5/7)^6•(3/7)^5. Доказать, что число (7n+1)^2-(2n-4)^2 делится на 15 при любом натуральном n.Решение задачи: Вычислить: 1) (35/48)^3•(6/7)^3•(1 3/5)^2; 2) (14/15)^4•(3/7)^4•(2,5)^3; 3) (5^3/6^2 )^4•(2/5)^5•(3/5)^7; 4) (7^4/?15?^2 )^3•(5/7)^6•(3/7)^5. Доказать, что число (7n+1)^2-(2n-4)^2 делится на 15 при любом натуральном n.
Решебник Колягин (2023) Алгебра
Навигация по заданиям
…363364365366367368369370371372373…

Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:

Вычислить:

1) (35/48)^3•(6/7)^3•(1 3/5)^2;

2) (14/15)^4•(3/7)^4•(2,5)^3;

3) (5^3/6^2 )^4•(2/5)^5•(3/5)^7;

4) (7^4/?15?^2 )^3•(5/7)^6•(3/7)^5.

Доказать, что число (7n+1)^2-(2n-4)^2 делится на 15 при любом натуральном n.