4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс

Упражнение 504 ГДЗ Колягин Ткачёва 7 класс (Алгебра)

Решить уравнение: 1) x^2-2x=0; 2) 3x+x^2=0; 3) 5x^2+3x=0; 4) x^2 (x-2)-2x(x-2)^2=0; 5) 3x(1-x)^2-x^2 (1-x)=0. Доказать, что если x+1/x=a, то x^3+1/x^3 =a(a^2-3).


Решебник Колягин (2023) Алгебра

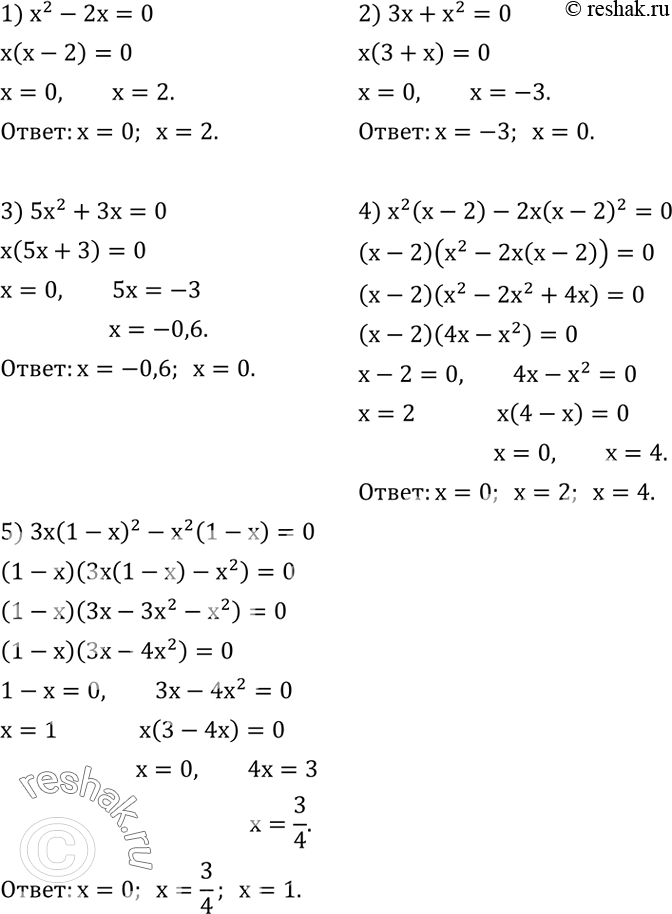
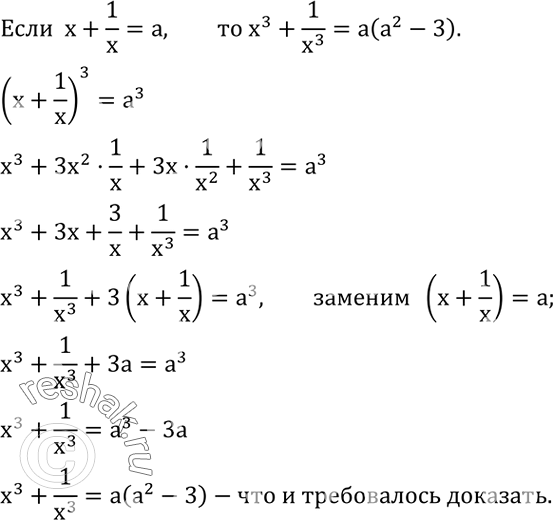
Решение задачи: Решить уравнение: 1) x^2-2x=0; 2) 3x+x^2=0; 3) 5x^2+3x=0; 4) x^2 (x-2)-2x(x-2)^2=0; 5) 3x(1-x)^2-x^2 (1-x)=0. Доказать, что если x+1/x=a, то x^3+1/x^3 =a(a^2-3).Решение задачи: Решить уравнение: 1) x^2-2x=0; 2) 3x+x^2=0; 3) 5x^2+3x=0; 4) x^2 (x-2)-2x(x-2)^2=0; 5) 3x(1-x)^2-x^2 (1-x)=0. Доказать, что если x+1/x=a, то x^3+1/x^3 =a(a^2-3).
Решебник Колягин (2023) Алгебра
Навигация по заданиям
…499500501502503504505УстноВводные506507…

Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:

Решить уравнение:

1) x^2-2x=0;

2) 3x+x^2=0;

3) 5x^2+3x=0;

4) x^2 (x-2)-2x(x-2)^2=0;

5) 3x(1-x)^2-x^2 (1-x)=0.

Доказать, что если x+1/x=a, то x^3+1/x^3 =a(a^2-3).