Упражнение 709 ГДЗ Колягин Ткачёва 7 класс (Алгебра)
Способом алгебраического сложения решить систему уравнений: 1) {(5(x+1)=2y+6 3(x-1)=3y-6)+ 2) {(1-3y=2(x-2) 1-3x=3y-2)+ 3) {(4(x-2)-3(y+3)=1 3(x+2)-2(x-y)=5)+ 4) {(7(2x+y)-5(3x+y)=6 3(x+2y)-2(x+3y)=-6)+ Из коробки, содержащей 8 мелков восьми различных цветов, Гена и Таня берут по одному мелку.
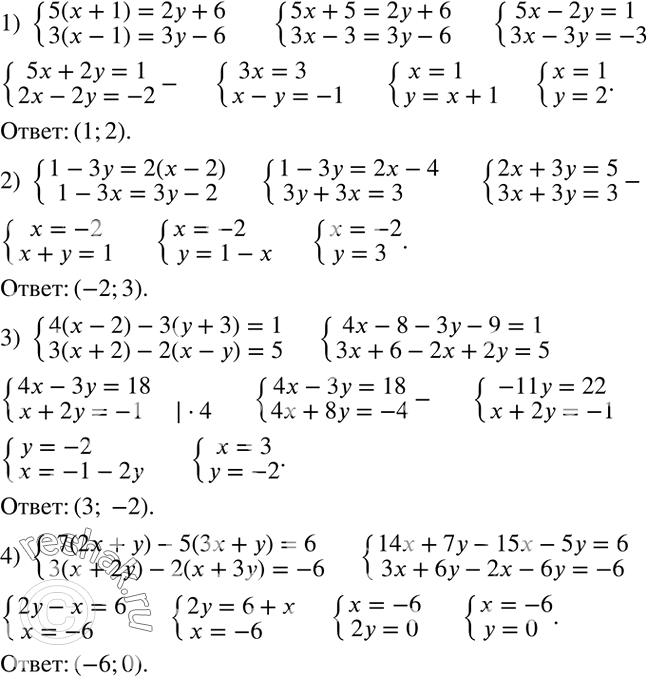

Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:
Способом алгебраического сложения решить систему уравнений:
1) {(5(x+1)=2y+6
3(x-1)=3y-6)+
2) {(1-3y=2(x-2)
1-3x=3y-2)+
3) {(4(x-2)-3(y+3)=1
3(x+2)-2(x-y)=5)+
4) {(7(2x+y)-5(3x+y)=6
3(x+2y)-2(x+3y)=-6)+
Из коробки, содержащей 8 мелков восьми различных цветов, Гена и Таня берут по одному мелку. Сколько существует различных вариантов такого выбора двух мелков?
