Практические и прикладные задачи Глава 2 ГДЗ Колягин Ткачёва 7 класс (Алгебра)

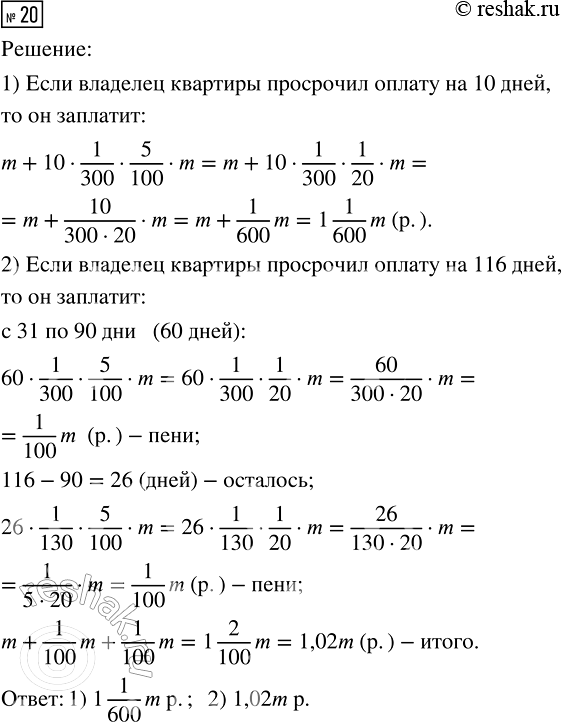
Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:

Сливочное мороженное на 90 % состоит из воды. Сколько воды содержится в 200 г такого мороженого?

2. Профессор испек шарлотку (яблочный пирог), в котором было 60 % яблок, а остальное - тесто. При этом 30 % теста составляли яйца и сахар, остальное - мука. Вся масса пирога равна 1,2 кг. Какова масса муки в пироге?

3. У рабочего заработная плата N р. С нее удержали 13 % подоходного налога. Какую сумму получил рабочий после этого?

4. После вычета 13 % подоходного налога служащий получил K р. Какая заработная плата была начислена служащему?

5. После вычета 13 % подоходного налога менеджер заплатил 20 % от оставшихся денег в счет погашения кредита. Какую сумму заплатил менеджер, если ему была начислена зарплата P р.?

6. Вова третью часть суток спит, 1,5 ч тратит на прием пищи, n ч - на учебу, m мин - на дорогу. Сколько времени ежедневно остается у него на другие дела (известно, что такое время у него остается)?

7. Потери в проводах транспортируемой электроэнергии достигают m %. Сколько электроэнергии доходит до потребителя, если электростанция вырабатывает P мегаватт электроэнергии?

8. Земельная полоса шириной a м и длиной b км нарезана на k одинаковых участков прямоугольной формы со стороной a м. Найи площадь каждого участка.

9. Мощность электрического прибора P находится по формуле P=UI, где I - сила проходящего через прибор тока, U - напряжение на приборе. При этом известно, что силу тока можно найти на формуле I=U/R, где R - сопротивление прибора. Выразить мощность прибора через: 1) I и R; 2) U и R.

10. Площадь S треугольника находят по формуле S=ah/2, где a - основание треугольника, h - его высота (рис.1). Найти: 1) высоту треугольника, если его площадь равна 25 см^2, а основание - 10 см; 2) основание треугольника, если его высота равна 80 мм, а площадь - 60 см^2.

11. Найти средний рост мальчиков класса, если результаты измерения их роста (в сантиметрах) оказались следующими:

1) 162, 167, 160, 170, 168, 162, 163, 164;

2) 158, 161, 169, 171, 160, 166, 165, 168, 166, 164.

12. Найтие среднее значение температуры (измеряемую в полдень) за первую декаду июля, если ежедневные замеры были следующими:

1) ?27?^о; ?28?^о; ?28?^о; ?29?^о; ?24?^о; ?24?^о; ?25?^о; ?26?^о; ?25?^о; ?24?^о;

2) ?29?^о; ?29?^о; ?31?^о; ?32?^о; ?32?^о; ?30?^о; ?28?^о; ?27?^о; ?26?^о; ?26?^о.

13. В мебельном магазине Ивану Петровичу захотелось измерить длину понравившегося дивана. Из-за отсутствия рулетки пришлось воспользоваться в качестве измерительных приборов подручными средствами: карандашом и монеткой. По длине дивана карандаш уместился 11 раз, а в оставшейся части 5 раз уместилась монетка. Дома Иван Петрович линейкой измерил длину карандаша и диаметр монеты. Размеры оказались 17,5 см и 1,1 см соответственно. Какова длина дивана?

14. Процентное содержание сахара в растворе, содержащем 0,3 кг сахара и 2,1 кг воды (рис.2), находят так:

p %=0,3/(0,3+2,1)•100 %=12,5 %. Каково процентное содержание сахара в растворе, полученном добавлением 400 г сахара в 3,6 кг воды?

15. Имеются три мерных отрезка известных длин a, b и c. При замере с их помощью длин сторон треугольника оказалось, что стороны выражаются через мерные отрезки следующим образом: 2a-b, 3a+c и 4b-c. Составить выражение для нахождения периметра треугольника и найти значение полученного выражения, если:

1) a=3 см, b=2 см, c=1 см; 2) a=4 см, b=3 см, c=2 см.

16. У бабушки на дачном участке стояли две большие бочки и имелись ведра двух видов: n-литровые и m-литровые. Для полива растений внук носил полными ведрами воду из пруда заполнял бочки. Первая бочка заполнилась, когда в нее влили пять n-литровых и семь m-литровых ведер воды. Во вторую бочку поместилась вода из шести n-литровых и пяти m-литровых ведер. Сколько всего литров воды подготовил внук для полива растений, если:

1) n=8/, m=5; 2) n=10, m=8?

17. Для полива овощей на огороде из полной 200-литровой бочки вычерпали восемь n-литровых и двенадцать m-литровых ведер воды. Сколько воды осталось в бочке, если:

1) n=10, m=5; 2) n=8, m=6?

18. Фирма-посредник, на счету которой было 10 млн.р., закупили в январе 150 компьютеров по цене a р., 70 пылесосов по цене b р. и 50 холодильников по цене c р. В феврале этого же года фирма закупила по тем же ценам 80 компьютеров, 50 пылесосов и 20 холодильников. Сколько денег осталось на счету этой фирмы к марту, если:

1) a=22 000, b=4 000, c=15 000; 2) a=17 000, b=3000, c=18 000?

19. Оплата коммунальных услуг рассчитывается следующим образом. Теплоснабжение за каждый квадратный метр - a р.; вывоз мусора - b р. с человека; водоснабжение - c р. с человека; радиоточка - d р. Какова оплата коммунальных услуг за содержание квартиры площадью S м^2, в которой проживают n человек? Рассчитать оплату, если:

1) S=43, n=3, a=30, b=50, c=200, d=25; 2) S=54, n=4, a=28, b=46, c=212, d=31.

20. За каждый просроченный месяц в оплате коммунальных услуг начисляется пеня в размере 0,5 % от суммы требуемого платежа. Какую сумму длжен будет заплатить владелец квартиры, забывший оплатить коммунальные услуги за один месяц в размере m рублей, если захочет погасить долг по прошествии 5 месяцев?

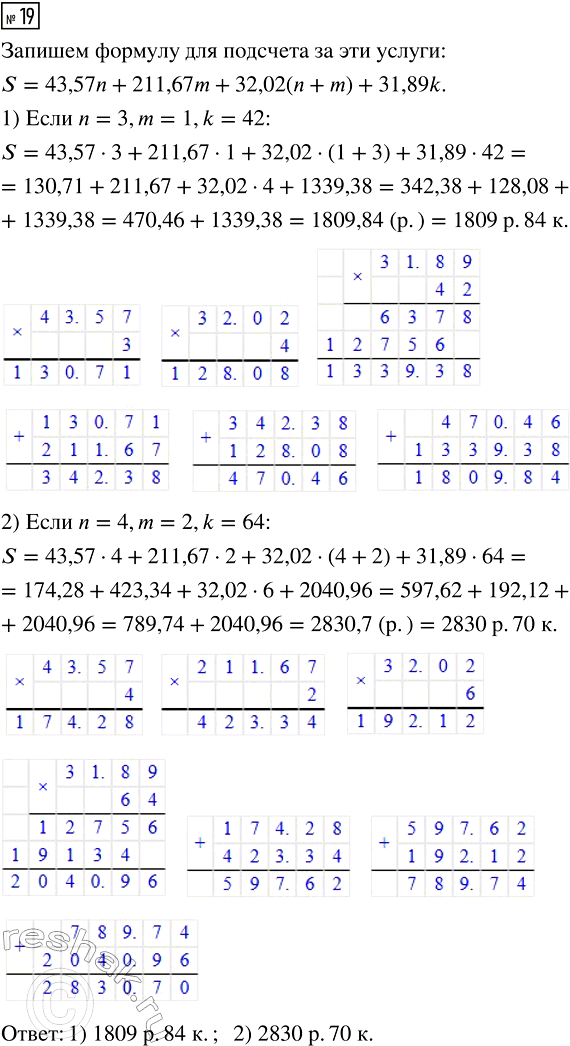
19. Оплата коммунальных услуг (без стоимости отопления) в 2021 году в Москве рассчитывалась следующим образом. Суммировалась оплата за холодное водоснабжение за n м^3 при тарифе 43,57 р./м^3, за горячее водоснабжение за m м^3 при тарифе 211,67 р./м^3, за водоотведение (n + m) м^3 при тарифе 32,02 р./м^3 и за содержание жилплощади k м^2 при тарифе 31,89 р./м^2. Записать формулу для подсчёта стоимости (S) за эти услуги. Рассчитать стоимость коммунальных услуг (без стоимости отопления), если:

1) n = 3, m = 1, k = 42; 2) n = 4, m = 2, k = 64.

20. За каждый просроченный день после 31-го дня от срока оплаты коммунальных услуг и по 90-й день включительно начисляются пени в размере 1/300 ставки рефинансирования Банка России. За каждый просроченный день, начиная с 91-го дня от срока оплаты, начисляются пени в размере 1/130 от ставки рефинансирования. Какую сумму заплатил владелец квартиры, если он просрочил оплату коммунальных услуг на 10 дней; на 116 дней? Известно, что в срок он должен был заплатить m рублей, а ставка рефинансирования в тот год составляла 5 % (процентная ставка рефинансирования при расчётах переводится в десятичную дробь).

Периметр равнобедренного треугольника равен 46 см. Найти стороны треугольника, если боковая сторона на 5 см больше основания.

2. В равнобедренном треугольнике основание составляет 0,4 боковой стороны. Найти стороны треугольника, если его периметр равен 36 см.

3. По всей границе земелного участка прямоугольной формы поставили забор. Ширина участка 150 м, а длина всего забора 1 км. Найти длину участка.

4. Вдоль границы участка прямоугольной формы, длина которого в 3 раза больше ширины, вырыли канаву длиной 240 м. Найти длину и ширину участка.

5. Из стальной проволоки диаметром 5 мм следует изготовить винтовую цилиндрическую пружину с целым числом витков и высотой 122 мм. Найти количество витков пружины, если зазор между витками пружины должен составлять 8 мм.

6. Ученик пишет заголовок газеты «Школьный бал». Длина листа 80 см, по 7 см он оставляет слева и справа от заголовка. Ширина каждой буквы и каждого просвета между словами в 2 раза больше просвета между буквами. Какой ширины получилась каждая буква в заголовке?

7. Во время стирки ткань садится на 1/16 по длине и на 1/18 по ширине. Сколько метров ткани шириной 90 см нужно приобрести, чтобы после стирки иметь 51 м^2 материала?

8. Фирма выпускает кофемолки, которые она предполагает реализовать по цене 3000 р. (за штуку). На приобретение деталей для изготовления одной кофемолки фирма тратит 1800 р., а за аренду помещения, зарплату сотрудникам и рекламу фирма платит 3 000 000 р. ежегодно. Считая, что других статей расходов у фирмы нет, определить, какое минимальное количество кофемолок должна реализовать фирма ежегодно, чтобы не нести убытков.

9. Три фирмы продали 236 компьютеров. Вторая фирма продала на 10 % больше компьютеров, чем первая, а третья - на 100 компьютеров меньше, чем первые две вместе. Сколько компьютеров продала каждая фирма?

10. Фирма A, B и C владеют 75 % всех акций некоторого предприятия. Количества их акций находятся в отношениях 4 : 12 : 9. Остальные 150 000 акций принадлежат работникам предприятия. Сколькими акциями владеет каждая фирма?