Упражнение 11.14 ГДЗ Мордкович Семенов 9 класс (Алгебра)
11.14. Дано выражение f(x)=(x+1)^2(x+3)(3x-17)/(x(2x-1)). При каких значениях переменной справедливо условие: а) f(x) > 0; в) f(x) б) f(x)?0; г) f(x)?0? *Цитирирование задания со ссылкой на учебник производится исключительно в учебных целях для лучшего понимания разбора решения задания.
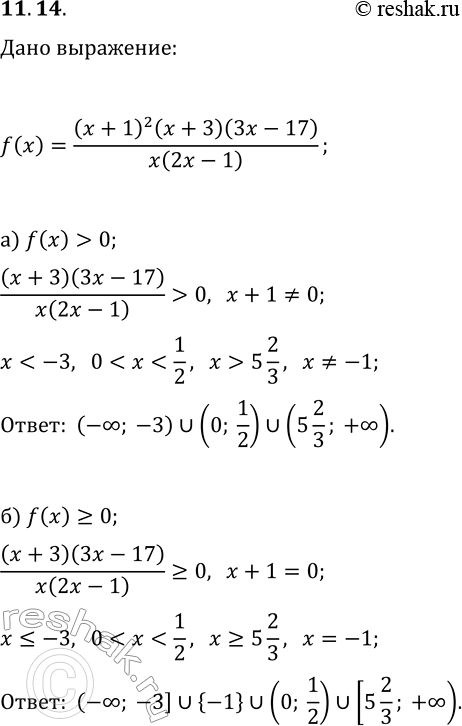
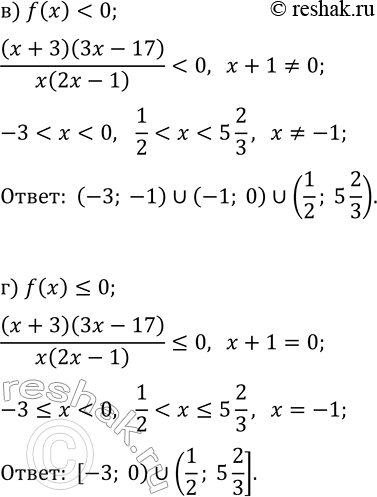
Ниже вариант решения задания из учебника Мордкович, Семенов, Александрова 9 класс, Бином:
11.14. Дано выражение f(x)=(x+1)^2(x+3)(3x-17)/(x(2x-1)). При каких значениях переменной справедливо условие:
а) f(x) > 0; в) f(x)
б) f(x)?0; г) f(x)?0?
