4 класс 5 класс 6 класс 7 класс 8 класс 9 класс 10 класс 11 класс

Упражнение 441 ГДЗ Колягин Ткачёва 7 класс (Алгебра)

Доказать, что если a(b+1)+b(a+1)=(a+1)(b+1), то ab=1.Разложить на множители числитель и знаменатель дроби и сократить ее: 1) (a^2-b^2)/(a+b); 2) (a-b)/(a^2-b^2 ); 3) (4c^2-9x^2)/(2c-3x);


Решебник Колягин (2023) Алгебра

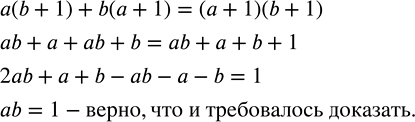
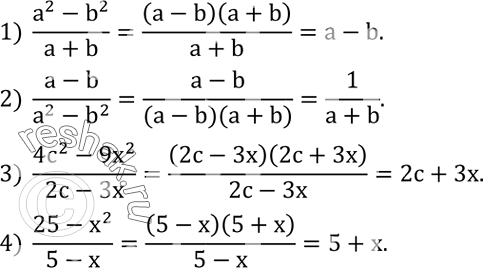
Решение задачи: Доказать, что если a(b+1)+b(a+1)=(a+1)(b+1), то ab=1.Разложить на множители числитель и знаменатель дроби и сократить ее: 1) (a^2-b^2)/(a+b); 2) (a-b)/(a^2-b^2 ); 3) (4c^2-9x^2)/(2c-3x);Решение задачи: Доказать, что если a(b+1)+b(a+1)=(a+1)(b+1), то ab=1.Разложить на множители числитель и знаменатель дроби и сократить ее: 1) (a^2-b^2)/(a+b); 2) (a-b)/(a^2-b^2 ); 3) (4c^2-9x^2)/(2c-3x);
Решебник Колягин (2023) Алгебра
Навигация по заданиям
…436437438439440441442443444УстноВводные…

Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:

Доказать, что если a(b+1)+b(a+1)=(a+1)(b+1), то ab=1.

Разложить на множители числитель и знаменатель дроби и сократить ее:

1) (a^2-b^2)/(a+b);

2) (a-b)/(a^2-b^2 );

3) (4c^2-9x^2)/(2c-3x);

4) (25-x^2)/(5-x).