Упражнение 31.12 ГДЗ Мордкович Семенов 9 класс (Алгебра)
31.12. Геометрическая прогрессия (b_n) задана формулой n-го члена. Найдите b_1 и q: а) b_n=0,1^(n+1); в) b_n=2/3·3^(2n-1); б) b_n=3·(v2)^n; г) b_n=5/2^(2n). *Цитирирование задания со ссылкой на учебник производится исключительно в учебных целях для лучшего понимания разбора решения задания.
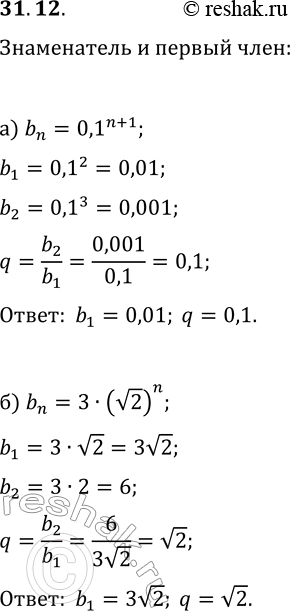
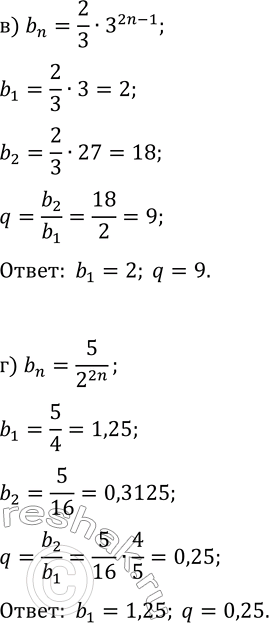
Ниже вариант решения задания из учебника Мордкович, Семенов, Александрова 9 класс, Бином:
31.12. Геометрическая прогрессия (b_n) задана формулой n-го члена. Найдите b_1 и q:
а) b_n=0,1^(n+1); в) b_n=2/3·3^(2n-1);
б) b_n=3·(v2)^n; г) b_n=5/2^(2n).
