Упражнение 217 ГДЗ Колягин Ткачёва 7 класс (Алгебра)

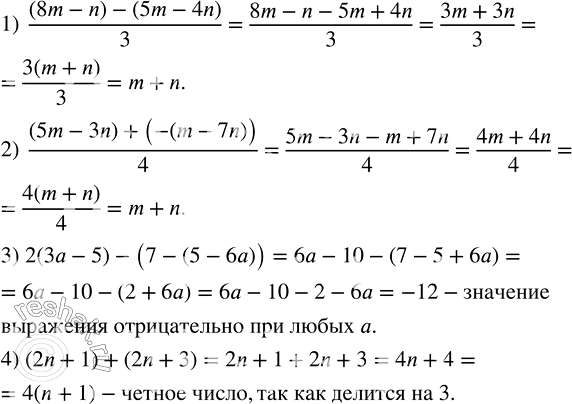
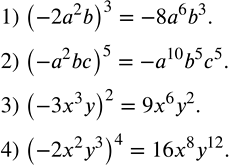
Ниже вариант решения задания из учебника Колягин, Ткачёва, Фёдорова 7 класс, Просвещение:

Доказать, что:

1) разность чисел 8m-n и 5m-4n делится на 3, если m и n - натуральные числа;

2) сумма числа 5m-3n и числа, противоположного числу m-7n, делится на 4, если m и n - натуральные числа;

3) при любых значениях a значение выражения 2(3a-5)-(7-(5-6a)) отрицательно;

4) сумма любых двух нечетных чисел является четным числом.

Возвести одночлен в степень:

1) (-2a^2 b)^3;

2) (-a^2 bc)^5;

3) (-3x^3 y)^2;

4) (-2x^2 y^3 )^4.